本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-03-15 18:14:52

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-04-10 20:33:40

【题目链接】

思路：

因为数据范围 $a , b \le 1000$ 很小，所以我们可以用一个数组来存一个数他出现的次数。

然后用两个数，储存数的 $l$ 最小值和 $r$ 的最大值。

依次枚举每个数，看看这个数出现的次数是否等与区间个数 $n$，如果是的话，就更新距离。

如果枚举完都没有一个满足条件的，输出 $-1$。

【AC记录】

AC code:

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010 , INF = 0x3f3f3f3f;
int a[N];\/\/存出现个数的数组
int ans = INF;\/\/答案，因为要区最小值，所以设成很大的值
bool t = false;\/\/判断是否输出-1 
int n , k , minl , maxr;
int main(){
	cin >> n >> k;
	for (int i = 1; i <= n; ++ i) {
		int l , r;\/\/区间的左右端点
		cin >> l >> r;
		if (l > r) swap (l , r);\/\/若l比r大，那么交换l，r 
		minl = min (minl , l);\/\/左端点的最小值
		maxr = max (maxr , r);\/\/右端点的最大值
		for (int j = l; j <= r; ++ j)
			a[j] ++;\/\/将这个区间里的数的出现次数++
	}
	for (int i = minl; i <= maxr; ++ i) \/\/枚举每一个数
		if (a[i] == n) {\/\/如果他是公共点
			ans = min (ans , abs(i - k));\/\/更新答案
			t = true;\/\/那么他就有公共节点，不用输出-1，把他设成false 
		}
	if (!t) puts("-1");\/\/如果他们没有公共区间，输出-1。 
	else cout << ans << endl;
	return 0;
}

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-04-10 20:59:05

【原题链接】

解题思路：

先按递减的顺序排序，然后依次枚举每个半径，因为他是一红一蓝一红一蓝......

所以每次枚举时 $i$ 要每次 $+2$。

求圆的面积需要知道 $π$,这里设 $PI = \operatorname{acos(-1)}$($\operatorname{acos()}$ 是反余弦函数，$\operatorname{acos(π)} = -1$，所以 $π = $ $\operatorname{acos(-1)}$)。

圆的面积计算方法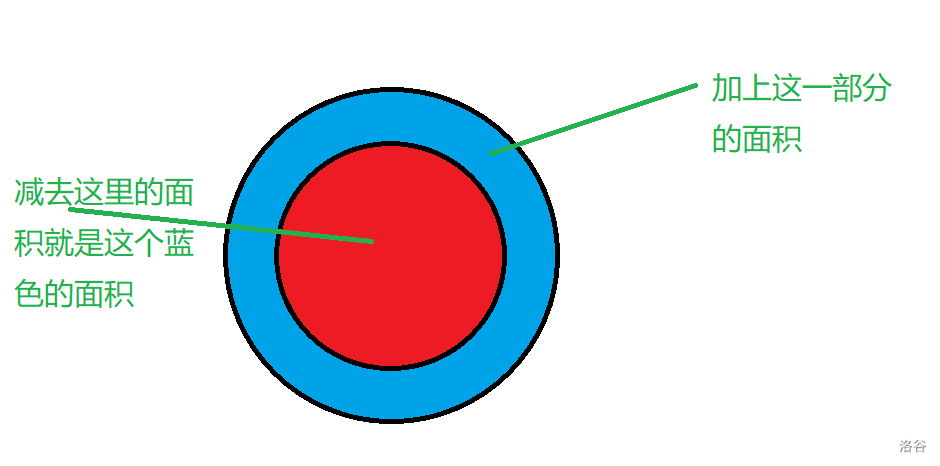： 【AC记录】

AC Code:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const double PI = acos(-1);
const int N = 110;
int n;
int r[N];
int main() {
    cin >> n;
    for (int i = 0; i < n; ++ i) cin >> r[i];
    sort (r , r + n , greater<int>());\/\/排序，按递减的顺序排 
    double res = 0;
    for (int i = 0; i < n; i += 2)\/\/因为红色的中间隔着一个蓝色的，所以每次i+=2 
        res += PI * (r[i] * r[i] - r[i + 1] * r[i + 1]);\/\/计算他的面积，用他本身的面积减去他包含的面积 
    printf ("%.6lf" , res);\/\/输出保留6为小数 
    return 0;
}

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-04-11 14:41:46

【题目链接】

题意：

给你 $n$ 堆石子，每次选三个数 $(i,j,k)$ 要求 $a_j \le 2$。

然后我们对 $(a_i , a_j , a_k)$ 进行一些操作：

$\left\{\begin{matrix} & a_j - 2\ & a_i + 1\ & a_k + 1 \end{matrix}\right.$

最后求让所有石子都在两边的最少操作次数，若无解，输出 $-1$。

题解思路：

我们先看看什么时候无解：

第一种无解的情况就是一共有 $3$ 堆，中间一堆还是奇数，那么我们只能选 $(1,2,3)$，那么只能从中间往左右分，中间怎么分总会剩一个，那么无解。

还有一种类似的情况： $(a，0，0，0，0，....，b，0，0，0，...，c)$，其中 $b$ 是奇数。 那么我们就可以把零都去掉，就变成了上一种情况，那么依旧无解。

还有一种就是所有的数都 $<2$，那么必定无解，输出 $-1$。

我们发现如果一个序列他有一个奇数，那么我们就要把一个数加到这个数上，比如： $(2,a,3,b,100)$ 此时，$3$ 是奇数，如果不给 $3$ 一个，那么 $3$ 怎么分也分不完。

就是若这个奇数前面多出来了 $2$，那么：

$(first , 2 , odd)$，我们让 $2$ 分出一个给第一个 $(first)$，另一个给这个奇数 $(odd)$，即 $odd + 1$，那么奇数的下一个就是偶数，那么这个奇数就变成了偶数。

若这个奇数的后面多出来了个 $2$，那么：

$(odd , 2 , last)$，我们让 $2$ 分出一个给最后一个 $(end)$，另一个给这个奇数 $(odd)$，那么这个奇数同样也可以变成偶数。

所以只要某个地方(当然不能是这个奇数的位置)多出来了一个 $2$，那么奇数的个数就 $-1$。

所以当一个奇数被填补之后，他就变成了一个偶数，他也能填补别的石子。

因为他被填补之后，他至少是 $2$ (因为他 $+1$ 了，所以不可能是 $0$ )，那么他就能继续填补别的奇数。

怎样证明他移动的次数是最少的呢？

对一个序列比如：

$(0 , 5 , 6 , 5 , 7)$，按照我们刚才的填法，那么对于每个奇数 $(第一个数以及最后一个数除外)$，最多会被填补一次。

因为他被填补成偶数时只会填补别的石子，而不再被填补，因为他本身就是偶数了。

那么操作成功的必要条件就是对于每个数 $a_i$，至少有一个 $\le 2$ 的。

当然若这个序列的长度为 $3$ 并且中间那个数是奇数的话，那么他 $\le 2$ 也没有用了。

【AC 记录】

AC Code:

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n;
long long a[N];
int main() {
	int T;
	cin >> T;
	while (T --) {
		cin >> n;
		for (int i = 1; i <= n; ++ i)
			cin >> a[i];
		int cnt1 = 0 , cnt0 = 0 , cnte = 0;\/\/cnt1是1的个数，用来判断是否无解
		\/\/cnt0是奇数的个数，cnte是偶数的个数，当然偶数不能为0，因为如果为零那么就不能填补
		for (int i = 2; i <= n - 1; ++ i) {\/\/第一个数和最后一个数不用动，所以从2开始，到n-1
			\/\/分别统计1，奇数，偶数不包含零的个数
			if (a[i] == 1)cnt1 ++;
			else if (a[i] % 2 == 0 && a[i] != 0) cnte ++;
			else if (a[i] % 2 == 1) cnt0 ++;
		}
		bool flag = (cnte) || ((cnt0) && (cnt0 + cnt1 >= 2));\/\/判断是否有解
		if (!flag) {
			puts("-1");\/\/若无解，输出-1
			continue;
		}
		long long ans = 0;
		for (int i = 2; i <= n - 1; ++ i) ans += (a[i] + 1) \/ 2;\/\/统计步数
		cout << ans << endl;
	}	
	return 0;
}

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2021-11-28 11:42:52

题目链接

题意

从一个长度为 $n$ 的序列中选出任意个，使这个序列的和非负，求这个序列的长度。

解题思路

输入，如果这个数就是非负整数，那么就加上这个数，否则就判断加上这个数是否为负数，如果不是负数，就将序列之和加上这个数，否则如果之前选的数比现在选这个数损失大，那么就把损失大的改成这个数。

AC code

废话少说，上代码：

#include <bits\/stdc++.h>\/\/万能头
using namespace std;
#define ll long long
inline int read() {\/\/快读模板 
	register char k = getchar();
	register int x = 0 , flg = 1;
	while (k < '0' || k > '9') {
		if (k == '-')flg = -1;
		k = getchar();
	}
	while (k >= '0' && k <= '9') {
		x = x * 10 + k - '0';
		k = getchar();
	}
	return x * flg;
}
inline void print(ll num) {\/\/快输模板 
	if (num < 0)putchar('-') , num = -num;
	if (num > 9)print(num \/ 10);
	putchar(num % 10 + '0');
} 
int n;\/\/有n个数 
int main() {
	n = read();
	priority_queue <int> q;\/\/大根堆 
	ll sum = 0 , ans = 0;\/\/sum是当前序列的和，ans是序列的长度 
	for (int i = 1 , a; i <= n; ++ i) {\/\/循环 
		a = read();\/\/输入 
		if (a >= 0) ++ans , sum += a;\/\/如果当前这个数本来就是非负的，那么就加上这个数，序列长度加一 
		else {
			if (abs(a) <= sum) {\/\/如果当前的和加上a还是非负的， 那么就加上这个数，序列长度加一 
				sum -= abs(a);\/\/减去个数 
				q.push(abs(a));\/\/加入大根堆 
				++ ans;\/\/序列长度加一 
			}else {
				if (!q.empty() && q.top() > abs(a)) {\/\/如果大根堆非空且之前选的数比这个负数小，就改成这个数 
					ll f = q.top();q.pop(); 
					sum += f - abs(a);\/\/换，因为是覆盖掉之前选的数，所以序列长度不加 
					q.push(abs(a));\/\/把当前更好的方案入堆 
				}
			}
		}
	}
	print(ans);\/\/输出序列长度 
	return 0;
}

第一篇题解，请求审核通过，同时如果有哪里有错请大佬指出。