本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-04-18 19:08:21

题解思路：

我们先扫描一遍 $s$ 和 $t$，然后如果啊 $s_{i} != t_{i}$，那么在 $t$ 中找到一个 $t_{j}$ 使得 $t_{j} == t_{i}$ 然后交换一下 $t_{j}$ 和 $s_{i}$。

我们看一下样例：

souse 和 houhe

它们按照上述法方只需要 $1$ 次就可以了。这是一种情况。

在看一个：

abc 和 bca

我们发现他第一个就不相等了，但 bca 里没有 $\ge 2$ 个 b，但我们可以：

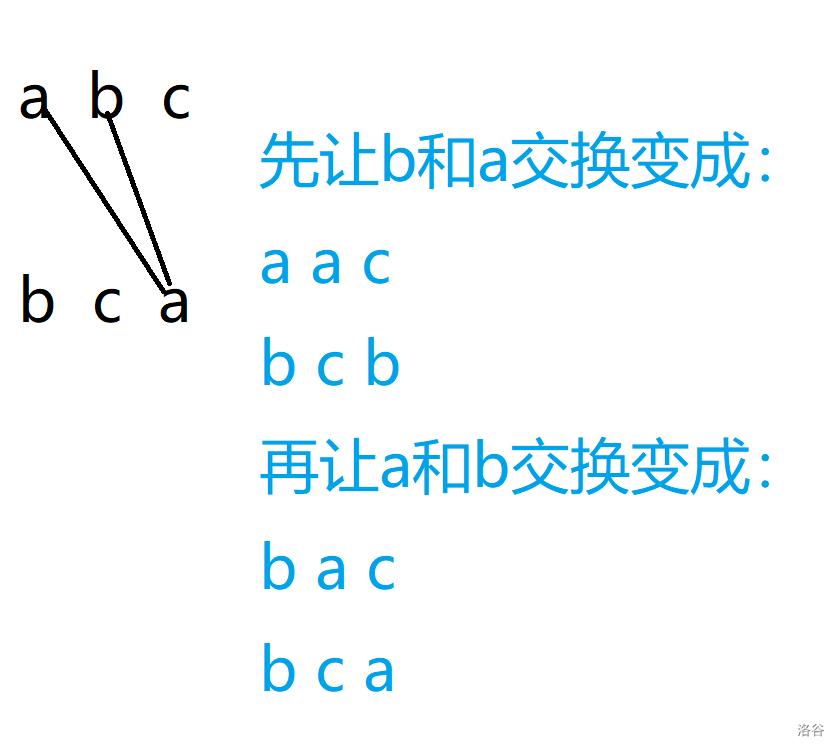
那么我们就可以把他首字母变成相等，一共用了 $2$ 步。

那我们就可以分两种情况来贪心：

• 1 若他们有一位不相等，并第二个串里有一个与他相等的字母，那么次数加 $1$。
• 2 若他们有一位不相等，而第二串里没有与他相等的字母，但第一个串里有一个跟第二个串里的字母相等的，答案加 $2$。

因为他至多每次都是情况 $2$，那么最多就执行 $n$ 次，所以执行次数一定 $\le 2n$。

AC CODE:

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
int n;
string s , t;
vector <pair <int , int>> op;
void solve () {
    op.clear();
    scanf ("%d" , &n);
    cin >> s >> t;
	for (int i = 0; i < s.size(); ++ i) {
		if (s[i] != t[i]) {\/\/若他们不相等 
			int flag = 0;
			for (int j = i + 1; j < t.size(); ++ j)
				if (t[j] == t[i]) {\/\/若有与他相等的 
					flag = 1;\/\/代表已经让s[i] == t[i]了 
					op.push_back ({i + 1 , j + 1});\/\/把操作加入到vector里 
					swap (s[i] , t[j]);\/\/交换 
					break;
				} 
			if (flag == 0) {\/\/若t串里没有与t[i]相等的则尝试方案二 
				for (int j = i + 1; j < s.size(); ++ j)
					if (s[j] == t[i]) {\/\/第二种情况 
						flag = 1;
						op.push_back ({j + 1 , t.size()});\/\/按照第二个情况进行操作 
						swap (s[j] , t[t.size() - 1]);
						op.push_back ({i + 1 , t.size()});
						swap (s[i] , t[t.size() - 1]);
					}
			}
			if (!flag) {\/\/如果这两种情况都不行，那么就无解 
				puts("NO");
				return ; 
			} 
		}
	}
	puts("YES");
	cout << op.size() << endl;\/\/一共有多少次操作，vector有一个好处就是可以自己通过size来知道他的长度，而数组就得用一个变量来储存。
	for (int i = 0; i < op.size(); ++ i) 
		cout << op[i].first << ' ' << op[i].second << endl;
}
int main() {
    int T;
    scanf ("%d" , &T);
    while (T --)
    	solve();
    return 0;
}