本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-05-02 14:44:08

题解思路：

样例：

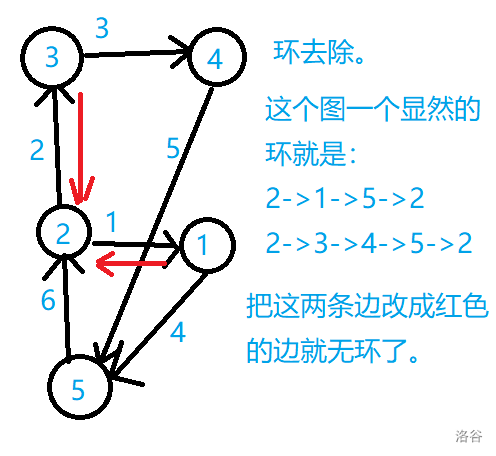
前置知识：

图中无环的条件是什么？

就是一个点无法走一圈回到自己，他就无环。

那么有一个算法：topsort（拓扑排序）

topsort 就会给每个节点一个拓扑值

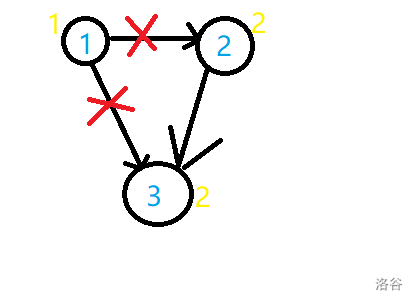
图例：

若一个图有环，那么他就没有拓扑序，因为他所有的点的入度都 $\ne 0$。

若一个点有一个起点终点 $\langle u , v\rangle$，若 $top_{u} < top_{v}$，那么这个图就是无环的。

或拓扑排序不能让他的入度为 $0$，那么他就是有环的。

然后我们来看一下这个题怎么做：

首先他让我们求最大值最小，那么根据经验应该是二分答案。

然后我们就上那方面上想。

把他得到的权值设成 $mid \longrightarrow$ 图中改变方向的边的权值最大值。

我们设 $w$ 为某个点的权值。

我们就先二分答案：

$w\le mid$ 不加进图，就相当于把他删掉。

$w > mid$ 按原样加进图。

判定：

若我们把 $\le mid$ 的边都删掉，他还是有环，那么就是删的边数太少了，那么把删边数的多一点。

若没有环了，就让答案的权值小一点。

若我们求出来了一个 $mid \longrightarrow$ 保证图中无环

$w \le mid$ 我们就把他看作无向边。

那么我们要反转那些边呢？？

拓扑排序出来的数组 $top$，若 $top_{u} > top_{v}$ 那么我们就反转这条边。

AC CODE

码字不易，求赞！