20251107-NOIP-模拟赛
题目概述
| 题目名称 | trape | candies | game | rcomb | redblue |
|---|---|---|---|---|---|
| 源文件名 | trape.cpp |
candies.cpp |
game.cpp |
rcomb.cpp |
redblue.cpp |
| 输入输出文件名 | trape.in/out |
candies.in/out |
game.in/out |
rcomb.in/out |
redblue.in/out |
| 时间限制 | 2 sec | 1 sec | 1 sec | 1sec | 2 sec |
| 空间限制 | 128 MB | 128 MB | 128 MB | 256 MB | 1024 MB |
| 题目类型 | 传统 | 传统 | Special Judge | 传统 | Special Judge |
| 是否开启 O2 优化 | 是 | 是 | 是 | 是 | 是 |
A. trape
背景
一个平面上有许多点,LYH 需要在这个平面上画一个等腰梯形,LYH 希望在这个梯形的点尽可能得多,LYH 让你帮她求梯形内最大点数。(点在梯形边上也算梯形内)

题目描述
给出 M 个点,求用一个上底长 $25$、下底长 $75$、高 $50$ 的等腰梯形最多能框住的点数。
输入格式
第一行两个正整数 N, M,N 表示横坐标在 [-N, N],纵坐标在 [-N, N] 的平面大小,M 表示点数。
接下来 M 行,每行两个整数 x, y,为各个点的横纵坐标。
输出格式
一行一个正整数为最大点数。
样例
输入
100 4
0 0
75 0
25 50
50 50输出
4数据范围
- 60% N <= 150
- 80% M <= 300
- 90% M <= 3000
- 100% N <= 2500, M <= 10000, -N <= x, y <= N
限制
- 2s
- 128M
B. Candies(candies)
题目描述
小 W 有 $N$ 堆糖果,每堆有 $a_i$ 个。现在,他要把这 $N$ 堆糖果分别分给 $N$ 个小朋友。为了使每个小朋友被分到的糖果数尽量均匀,小 W 每次会按顺序执行以下操作: 1. 找到糖果数量最多的糖果堆(如果多于一个,则随机选择一个),从中取出一颗糖果; 2. 在剩下各堆糖果中(包含前面取出糖果的那堆)找到糖果数量最少的糖果堆(如果多于一个,则随机选择一个),将刚刚取出的糖果放入这堆糖果中。
现在,小 W 想请你帮他计算,$K$ 次操作后,最终被分到糖果最多的小朋友与最少的小朋友,他们得到的糖果数之差(即操作后糖果最多的糖果堆中的糖果数与糖果最少的糖果堆中的糖果数之差)。
输入输出格式
输入格式
从文件 candies.in 中读入数据。
输入包含多组测试数据。
第一行包含一个正整数 $T$ ,表示该测试点的测试数据组数。
对于每组测试数据,第一行包含两个正整数 $N,K$ ,表示糖果的堆数和小 W 要进行的操作次数;第二行包含 $N$ 个正整数 $a_i$ ,表示每堆糖果初始时的糖果数。
输出格式
输出到文件 candies.out 中。
对于每个测试数据,输出一行包含一个正整数,表示该组测试数据的答案。
样例输入和输出
样例输入 1
2
4 100
1 1 10 10
4 3
2 2 2 2样例输出 1
1
0数据范围
对于 $10\%$ 的数据,$N\leq 500, K\leq 40000, a_i\leq 500$ ;
对于 $30\%$ 的数据,$N\leq 1000, K\leq 1.5\times 10^5, a_i\leq 1000$ ;
对于 $50\%$ 的数据, $N\leq 10000, K\leq 2\times 10^7, a_i\leq 10^5$ ;
对于 $100\%$ 的数据,$1\leq N\leq 10^5, 1\leq K \leq 1\times 10^{15}, 1\leq a_i\leq 10^9$ 。
B. Game(game)
题目描述
Alice 和 Bob 在玩一个游戏,Alice 和 Bob 各自控制着自己的队伍 A 和 B,假设军队中的人分布在一个一维数轴上。现在 Alice 和 Bob 每回合都可以做出一个行进指令:
以 Alice 为例,她可以让 A 队伍中的每个人都向前或向后移动 x 的距离,同理 Bob 也可以操作 B 队伍,进行一次行进。
现在告诉你战场的初始情况,即两个队伍中的人在数轴上的分布(但是我们并不知道每个人属于哪个阵营),以及经过一个回合后队伍中人的位置(只有一个回合),你需要求出 Alice 和 Bob 所做的行进指令是什么。
输入输出格式
输入格式
从文件 game.in 中输入数据。
第一行一个数$ n $,代表两个队伍中的人的总和。
第二行$ n $个整数,第$ i $个整数代表第$ i $ 个人的初始位置 $ x_i $。
第三行 $n$ 个整数,第$ i $个整数代表一个回合后各个人的位置 $y_i$。
$x_i $和 $y_i$ 不一定对应同一个人的位置。
数据保证不会有两个人处于同一个位置。
输出格式
输出到文件 game.out 中。
第一行一个数$ n$,代表两个队伍中的人的总和。
第二行$ n $个整数,第 $i$ 个整数代表第 $i$ 个人的初始位置 $x_i$。
第三行 $n $个整数,第$ i $个整数代表一个回合后第$i$个人的位置$ y_i$。
数据保证不会有两个人处于同一个位置。
样例输入和输出
样例输入 1
5
1 2 3 4 5
70 71 0 1 72样例输出 1
67 -1Alice 控制初始的$3,4,5$三个位置,操作后为$70,71 ,72$。
Bob 控制初始的$1, 2$两个位置,操作后为$0, 1$。
输出两个距离代表一个可能的行进指令。数据保证至少存在一个解。
数据范围
对于$ 30\% $的数据,$n≤100$;
对于 $70\%$ 的数据,$n≤1000$;
对于 $100\%$ 的数据,$n≤70000, 0≤x_i, y_i≤100000$。
C.Rcomb (rcomb)
题目描述
$Na$老师有$N$张卷子排成一列,第$i$张卷子有其难度$V_i$,由于$X$爷的出现,$Na$老师需要将这些卷子合并为$1$张 每次$Na$老师以相等的概率随机选择两张相邻卷子,消耗两张卷子难度和的体力,得到一张难度为两张卷子难度和的卷子,求$Na$老师需要消耗的体力期望值。
输入输出格式
输入格式
第一行:一个整数$N$。
第二行:$N$个整数$V_1、V_2、...、V_N$。
输出格式
只有一行,一个小数,表示(小数点后保留3位)表示$Na$老师需要消耗的体力期望值。
样例输入和输出
样例输入 1
2
1 1样例输出 1
2.000样例输入 2
4
1 2 3 4样例输出 2
21.667数据范围
对于 $20\%$ 的数据 $N \leq10$;
对于$ 40\%$ 的数据 $N\leq100$;
对于$ 80\%$ 的数据 $N\leq5000$;
对于 $100\% $的数据 $1\leq N \leq 500000 , 1 \leq V_i \leq 10000$.
E. 红蓝(redblue)
题目描述
在坐标平面上有 $N$ 个红色点和 $M$ 个蓝色点。给定自然数 $W$ 和 $H$。
第 $i$ 个 ($1 \leq i \leq N$) 红色点的坐标是 $(r_{xi}, r_{yi})$,第 $j$ 个 ($1 \leq j \leq M$) 蓝色点的坐标是 $(b_{xj}, b_{yj})$。
所有点的坐标都是不同的。
我们需要放置一个宽度为 $W$,高度为 $H$ 的矩形,该矩形的边与坐标轴平行,并且它的四个顶点是整数坐标。我们希望最大化矩形内包含的红色点与蓝色点数量之差。
矩形包含点的条件是:如果矩形的左下角坐标为 $(a, b)$,且点的坐标为 $(x, y)$,那么该点包含在矩形内当且仅当满足 $a \leq x \leq a+W$ 且 $b \leq y \leq b+H$。
我们要求得这个差值的最大值,并找到符合这个最大差值的矩形位置。
下图展示了在平面上有 3 个红色点和 4 个蓝色点的情况。为了说明问题,红色点用圆圈表示,蓝色点用三角形表示。
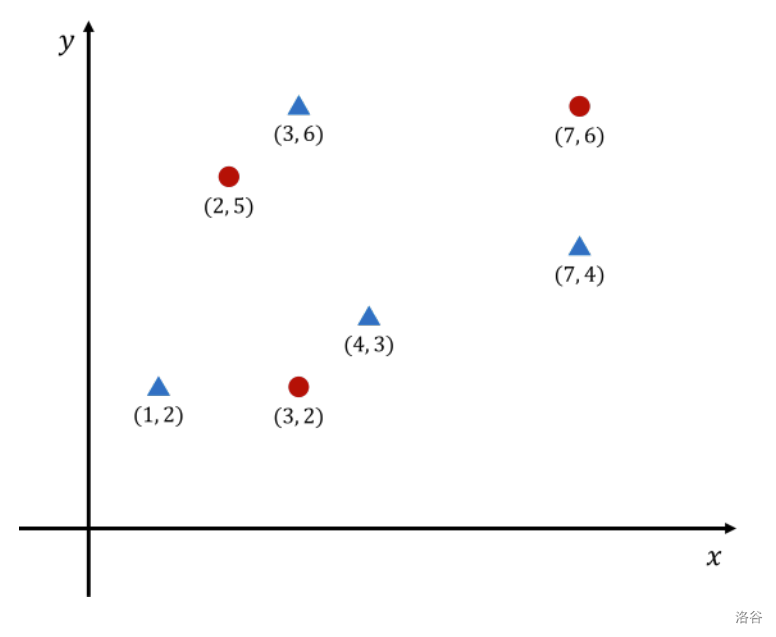
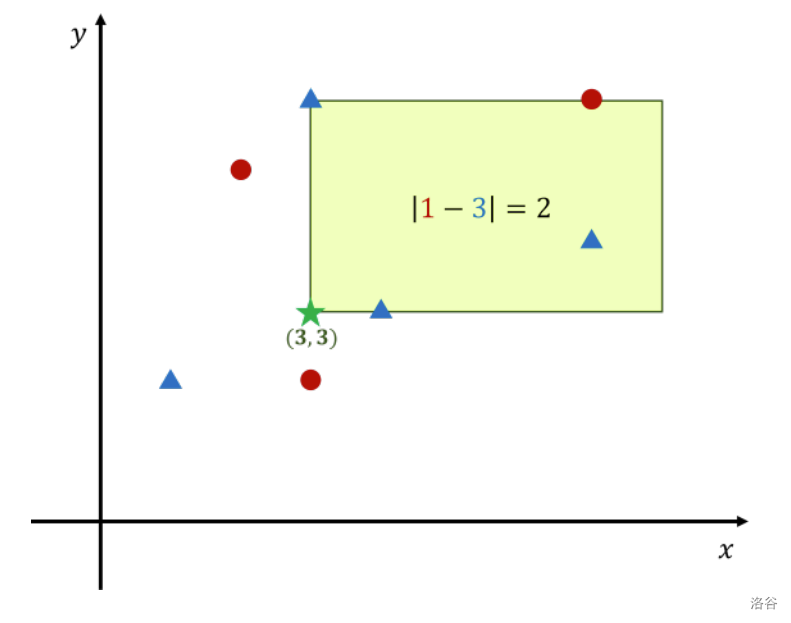
假设 $W = 5$,$H = 3$,那么如果将矩形的左下角放在 $(3, 3)$,矩形内包含 1 个红色点和 3 个蓝色点,这时点的数量差为 2。无论矩形放置在哪里,点的数量差都不会大于 3,因此答案是 2。
输入格式
第一行给出整数 $N$ 和 $M$,以及矩形的宽度 $W$ 和高度 $H$。
接下来的 $N$ 行,每行包含一个红色点的坐标 $(r_{xi}, r_{yi})$。
接下来的 $M$ 行,每行包含一个蓝色点的坐标 $(b_{xj}, b_{yj})$。
输出格式
输出一个整数,表示最大点数差值。然后输出矩形左下角的坐标 $(a, b)$。
如果答案有多个,输出任意一个即可。
输入输出样例 #1
输入 #1
3 4 5 3
3 2
2 5
7 6
1 2
4 3
3 6
7 4输出 #1
2
3 3输入输出样例 #2
输入 #2
3 3 4 4
1 1
2 2
3 3
1 3
3 1
4 4输出 #2
2
-2 -2说明/提示
约束条件
- $1 \leq N, M \leq 100\,000$
- $1 \leq W, H \leq 10^9$
- $1 \leq r_{xi}, r_{yi} \leq 10^9$ ($1 \leq i \leq N$)
- $1 \leq b_{xj}, b_{yj} \leq 10^9$ ($1 \leq j \leq M$)
子任务
- (10 分)$1 \leq N, M, W, H, r_{xi}, r_{yi}, b_{xj}, b_{yj} \leq 50$
- (15分)$1 \leq N, M, W, H, r_{xi}, r_{yi}, b_{xj}, b_{yj} \leq 1\,000$
- (15 分)$1 \leq N, M \leq 100$
- (10 分)$1 \leq N, M \leq 1\,000$
- (50 分)无额外约束条件

 鲁ICP备2025150228号
鲁ICP备2025150228号