https://www.luogu.me/article/ki71nw88
声明
本文非严谨的算法理论研究,仅仅是个人对解题经验的归纳和实验性的系统总结,不保证理论上的完备性与纯粹性。仅对解题实践提供一个较为自洽的解释,作为参考。
本文所有题都不会提供题意和完整包含细节的题解,也就是说您需要先做一遍或看其他题解,因为没有做题经验就无法感受解题思想。您也可以把本文理解成一个归类好的题单。
如果一题包含多项技巧则会放在多处,但如果包含多项思想则只会在一处解说,其余处记入“其他”项并打+号。如果出现一题多解会记入多个类别并多次解说。有些不是非常典型或过难过易的题也会记入“其他”项。
带括号的题是内部训练题或经典问题。
如果您认为一些理论表述有偏颇,或找到文章无法解释的题目(反例),可以告诉我。
本文会时常更新。
引言
dp 在 OI 中应用之广,变化之多,难度之大,已使它不再仅限于原先 "dynamic programming" 的定义和特质。《算法导论》给了 dp 一个严谨的基本定义,但缺乏实操性和可扩展性。本文不会采用算导中的描述方法,而是用一个解题方法论的方式展开,但是也会牵涉到一些基本定义及术语。因此,在阅读本文前,您应当先掌握算导第 15 章(动态规划)的内容。
在 OI 中,狭义的 dp 基于的是一个类自动机结构(一般生成过程只有串联和并联两种,串联就是在自动机上走,并联可以理解成多维状态的降维,我不清楚这个东西有没有更形式化的描述)。考虑某种组合结构,所有满足某一条件的该结构作为元素(称为“解”)组成一个解集,题意要求求出这些解的某种权值经过某种运算后的结果。dp 就是使得自动机在这些解上运行。这种情况下的 dp 大致有三类:最优化、计数、判定。在所有合法解不漏的前提下,它们需要满足的关键条件是:最优子结构、不计重、无。
广义上来说,习惯于将大部分用递推解决问题的方法都称作 dp。
可以大致限定一下狭义 dp 的使用范围:如果可以找到一种生成方式,能恰好(逐步)刻画出所有满足条件的解,并且中途为了判定符合条件以及为了辅助求出权值所记录的信息是局部的或可能性较少的,那就有机会使用 dp。当然进一步地,如果有更好的结论能刻画模型,使得无需逐步生成解(解的可能性只有 $\mathrm{O}(1)$ 种或可以通过某类极简单的方式生成),那就是贪心、构造、直接计数或其他无算法题了。
dp 题的核心就是对原问题模型的分析、转化、拆解和重构,通过钦定生成的顺序以及分析其变化的本质,将原先可能性极多的解“少量多次”地用变量来描述从而解决。
下面我会从一些特殊类型的 dp 技巧和通用 dp 解题方法两方面,介绍如何思考 dp 题。由于 dp 的设计思想较细较杂,故有一些小的思想和套路不会单独写出来,而是会在例题讲解的最后一段,我会将它加粗。
本文(将)是我的集训队论文的素材来源,预计论文对方法论的叙述方式可能与本文有出入,您可以结合着看。与论文有关的注释以 "remark." 开头。
基于特殊结构的技巧
决策单调性优化与 ds 优化等的具体技术详见下一章。
括号序列
括号序列的生成思路一般有以下几种:
- 直接按下标,记录当前多的 $\texttt{(}$ 数。
- 按外层配对括号 $\texttt{(...)(...)...(...)}$ 拆开。
- 拆第一对配对括号,剩下视作整体 $\texttt{(...)...}$。
- 视作折线,进行容斥。
其中 2、3 是直接对着定义 dp,3 可以理解成对括号树三度化再 dp,会方便一些,同时避免计重。2 在最优化问题下可以随便选一个断点拆。
例
CF1781F:称第 $i$ 轮加入的为第 $i$ 组括号。这题由于增加了时间维度,故又多出几种思路,但直接按时间维 dp 是不行的:正着信息量太大,倒着会把同一组括号拆到两部分。不按时间 dp 的话考虑概率不方便,先求出方案数。
先分析一下题目条件的静态表述:把每个括号加入的时间写成序列,则不能出现 $[j,i,i,j],[i,j,i,j],[j,i,j,i]$(其中 $i
(解 1)考虑第一组括号,它们将序列切分成三部分,同一组括号在同一部分。这样只需在记一维“当前段前面多的 $\texttt{(}$ 数”即可。由于是三部分,故是 $\mathrm{O}(n^4)$。先对其中两个卷积即可做到 $\mathrm{O}(n^3)$。
(解 2)尝试方式 3,问题在于这对匹配的括号可能不是同一组。那就改成找与开头括号同一组的括号,它将序列切成两部分,同一组括号在同一部分,第一部分都后于开头括号加入。dp 状态与第一种相同,直接三次方。
一些类括号序列的结构,主要依据递归定义来 dp(定义可能不唯一)。主要找形式相同的子问题。
例
CF888F:断环为链,直觉上来说结构属于以下两种(红色的是边):
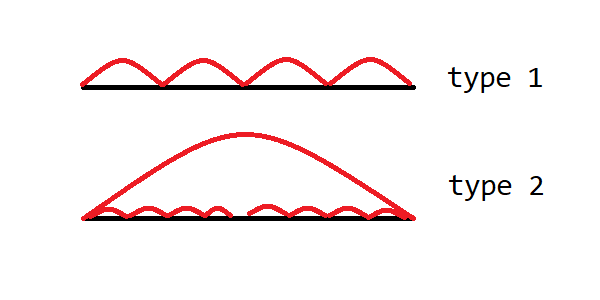
一种是在两种类型之间交替 dp,type 1 按方式 3 转移,type 2 找中间断点。另一种是只对 type 2 dp,即先逐步确定左侧的子结构,到达断点后再右侧(如果每次随意转移左右侧则会计重)。
CF913E:这题多了个优先级,dp 得记当前表达式的层级。我的具体思路是记能否被 T 或 F 识别(最外层是否没有 $\texttt{or}$),转移有几种:$\texttt{or}$ 连接、$\texttt{and}$ 连接、加 $\texttt{()}$、加 $\texttt{!()}$。由于后效性得多轮松弛。
另一个跟 01 序列相关的罕见技巧也放这(来源于 dmy WC2022 讲课的 PA2021R2T1(lgP9047)):如果有一些 0 和一些 1,每个都有权值,要选一个子集 01 数量相同,最优化权值相关某个东西,可以把元素随机打乱再 dp,记录当前 0 比 1 多多少,这一维可以只开到 $\Theta(\sqrt n)$。
排列
这一节侧重于排列未知的情况。
排列的关键是找到一个生成顺序,使得已生成部分的数不需要逐个记录,而只需抽象成少量的几个量。最基本的排列生成顺序如下:
|
预定(绝对) |
插入(相对) |
| 按下标 |
从左往右逐一确定值 |
从左往右逐一确定当前值在前缀中排第几大 |
| 按值 |
从小到大逐一确定位置 |
从小到大逐一插入排列 |
还有几个典型的应用。一种是只对一个单调子序列 dp,剩余部分直接用组合数确定(属于按值、断点);一种是基于笛卡尔树或类似笛卡尔树的分治结构,合并时确定相对大小,乘组合数(属于按值、预定、单步)。
例
CF1806D:(解 1)对答案有贡献的是所有 $p_i=\operatorname{mex}_{j
(解 2)尝试按值、插入、单步转移。如果 $i$ 不插到末尾则无影响,否则当且仅当 $1\sim i-1$ 操作结束后根仍为 $1$ 且 $a_i=0$ 时有贡献。从另一个角度看,这个解法的处理是把每个点的贡献拆开,将原所求转化为容易转移的“前 $i$ 个点操作后根仍为 $1$ 的方案数”,属于拆分要素。
CF1437F:可以线性。对更新前缀 $\max$ 的值 dp。如果从大到小 dp,就是 $f_i$ 每次从 $2a_j\ge a_i$ 的 $f_j$ 转移,并在 $j$ 之后插入范围在 $(a_i/2,a_j/2]$ 的剩余 $a$,同样可以换元做到线性。这属于按值、插入、断点转移。
如果从小到大 dp,就必须按值、预定、断点转移。当 $f_i$ 从 $f_j$ 转移时,$a_i$ 塞到第一个空位,后面的空位选填 $(a_j/2,a_i/2]$ 中的剩余 $a$。注意到这个问题中的两个两倍是有意义的,如果两个倍数不同,可能导致“剩余 $a$”数量无法确定。
本题具体 dp 方程详见概率 & 期望一节。
USACO21DECPlatinumT3:(解 1)同样,对猜的数 dp,处于转移之间的无用数直接用组合数算。官方解法是先对答案的期望 dp,这样可以避免 dp 同时要记方案数(这个技巧详见后)。前缀和优化即可。这也属于按值、断点转移。
(解 2)尝试按下标、插入、单步转移,即每次在末尾加入一个数,不妨设是 $\le x$ 的,那么只需要分它会被猜和被忽略两种情况即可。这个同样可以期望化以省掉方案数 dp。
这三个例子本质上是形如“确定了主要元素(某个单调子序列),剩余元素必须出现在某个主要元素前或后”,为了使状态维数小,就对主要元素 dp。这时剩余元素的位置应当在对应的主要元素被 dp 到时用数学方法确定。如果限制方向与 dp 方向相同则用预定法,否则用插入法。
CF1363F:问题转化为找到一个排列 $p$,使 $s_i=t_{p_i}$ 且 $\sum_i[\max_{j
CF1799G:如果不容斥至少得 $\mathrm{O}(n^5)$。容斥的话麻烦的一点是,如果一组内有多个钦定不合法的投票,它们的方案数无法确定(类似一个有上限的整数拆分)。这里的一个技巧是,把投给同一个人的票也视作有先后顺序,这样投票方案就变成了一个排列,最后除以 $\prod c_i!$ 即可。这样直接枚举组内钦定数,然后用组合数即可。
- CF1439D:正反 dp 要记的信息量都太大,考虑到多个占用位置极长连续段之间是无关的,因此可以分开 dp。对于一个连续段,考虑其最后一个人,拆成两段即可。段的合并或并列就乘组合数确定相对大小。
其他. +CF1784D、+CF856C、ABC134F
背包
基础的背包技巧包括:
- 多重背包的二进制拆分和同余转移。
- 换维。价值较小时可以定义状态为得到 $i$ 的价值至少要多少重量。
- 物品大小和有限制时只有根号种物品。
- 无序整数拆分相关的两个:“全体 +1 & 新开一个”的转移方式,以及按下标 dp 总状态数为 $n^2\ln n$。
- 从 GF 角度考虑。
- 同余最短路。
例
(经典问题)(无序整数拆分):除了五边形数解法外,还有一种 $1.5$ 次的。对于 $\le\sqrt n$ 的数,直接完全背包,$>\sqrt n$ 的数少于 $\sqrt n$ 个,套用平方的做法,$f_{i,j}$ 表示 $i$ 个数和为 $j$,每次加入单个 $1$ 或全体加 $1$,最后全体加 $\sqrt n$,两类卷起来即可。
CF1425B:情况只会有两种:两人在某个环上卡住、两人分工将所有环走完(且最终至少有一人停在点 $1$)。后者简单。前者需要枚举卡住的环,这时相当于求 $\prod_{j\ne i}\left(x^{l_j}+1+x^{-l_j}\right)$ 某一区间的系数,可以预处理前后缀乘积拼合,也可以预处理所有的积然后 $\mathrm{O}(n)$ 除以当前的因式,都是 $\mathrm{O}(n^2)$ 的。只利用环大小只有 $\mathrm{O}(\sqrt n)$ 种也可以优化成 $\mathrm{O}(n^2)$,但上述两种技巧不能同时优化,变成 $\mathrm{O}(n\sqrt n)$。
CF1442D:容易用调整法证明只有一个数组选一部分,其余要么全选要么全不选。于是问题就变成了 $[x^k]\sum_iA_i(x)\cdot\prod_{j\ne i}\left(1+s_jx^{t_j}\right)$ 的 $(\max,+)$ 卷积版本。这不适用于例 1 的两种处理方法,因为前后缀拼合会由于 $A_i(x)$ 没有简单形式而必须把每一项算出来,就得 $\mathrm{O}(k^2)$,而本题没有可减性,不能作除法。这时可以利用分治方法做到 $\mathrm{O}(nk\log n)$。这个方法也可以用到上一题,做到 $\mathrm{O}(n^2\log n)$ 或 $\mathrm{O}(n^2)$(如果分治时控制多项式次数得当)。
CF1740F:充要条件是前 $k$ 大的 $\text{size}$ 之和 $\le \sum\min(cnt_i,k)=s_k$。$f_{i,j,k}$ 表示前 $i$ 大,和为 $j$,目前 $k$,$ik\le j$,状态总数 $\mathrm{O}(n^2\log n)$,转移可以做到 $\mathrm{O}(1)$(新加一个数或 $k$ 减一)。用“全体 +1 & 新开一个”的转移思路也是可以的:$g_{i,j,k}$ 表示已确定 $i$ 个,和为 $j$,还能全体加至多 $k$ 次,其中 $k\le s_i/i$。
[十二省联考 2019] 皮配:正常的暴力 dp 可以记录红阵营和 R 派系的选手数。用 GF 解释就是,一个城市会贡献 $\left(1+x^{\sum s_i}\right)\prod(1+y^{s_i})$,这意味着除了有偏好的城市以外,其余的可以分离阵营和派系两个要素。有偏好的城市贡献形如 $\prod_{i\notin T}(1+y^{s_i})\cdot \left(A(y)+B(y)x^{\sum s_i}\right)$($T$ 为有偏好的学校)。一个大致的思路是把后面特殊的部分全部卷起来(记作 $E(x,y)$),这样需要 $\mathrm{O}(k^2s^2M)$。但由于 $A,B$ 都是若干单项和二项式的积,故分别可以逐一乘(求出 $E(x,y)A(y)$ 和 $E(x,y)B(y)$),然后最后再决定阵营,即 $E\cdot A+E\cdot B\cdot x^{\sum s_i}$。最终没必要把 $E$ 和 $x,y$ 剩余整齐部分卷起来,只需要枚举 $E$ 的每一项,然后乘上两段系数和的积即可。
这题的几个技巧是:逐个乘项数小的多项式一般比先把这些小多项式乘起来再统一卷更优;求最终答案时可以视作求卷积的单点值,避免全体卷积;同时,对于这类最终不使用多项式算法的背包题,不能完全抛弃组合意义,要结合代数和原模型推导,否则可能会丢失方向或性质。
然后有几个很牛的技巧(仅用于最优化):
完全背包的倍增方法。当容量 $T$ 很大,最大重量 $W$ 较小时,通过将解按重量排序交替放,可证明一定能将解拆成两个总重量差 $\le W$ 的部分,于是求出 $[T-W,T+W]$ 的最优解可以 $\mathrm{O}(W^2)$ 递推到 $[2T-W,2T+W]$。如果额外对选的数量 $C$ 有限制,同样可以证明一定能将解拆成两个总重量差 $\le W$ 且数量差 $\le [2\nmid C]$ 的部分,从而有两种转移方式:一种是如果 $C$ 为奇数就转移单个,否则直接对半,这样做为了保证状态的封闭性就得求 $[T-2W,T+W]$ 的最优解;另一种是直接对于 $\lfloor C/2\rfloor$ 和 $\lceil C/2\rceil$ 的数量要求都 dp 即可。无论如何都会多一倍常数。
只有完全背包能这么搞。$\mathrm{O}(nT)\rightarrow\mathrm{O}(W^2\log T)$。
背包的贪心性质。考虑按性价比贪心选直到第一次遇到无法选的物品就停止,设选出的物品集合为 $G$,最优解为 $O$。有性质:存在 $O$ 使 $\lvert G\oplus O\rvert\le 2W$。
证明:考虑 $G$ 加删元素(不重复加删一个元素)逐渐变成 $O$ 的过程,容易维持重量和 $\in[T-W,T+W)$。如果 $\lvert G\oplus O\rvert>2W$,那么由鸽巢原理,一定存在两个中间状态重量和相等。由于 $G$ 选的是性价比最高的一些,故把这两个重量和相等的中间的加删部分去掉,一定不劣。
那么只需一个状态数为 $4W^2$ 的背包即可。$\mathrm{O}(nT)\rightarrow\mathrm{O}(nW^2)$。
如果价格最大值 $V$ 很小,也有类似的性质($\lvert G\oplus O\rvert\le 2V$),实现用换维技巧即可。
例
- (经典问题)(给定 $n$ 个数,选出一些使和 $\le T$ 且最大):先随意贪心选,问题转化为有正数和负数的情况,且剩余容量 $
- (物品)(有 $a_i$ 个数 $i$,$\lvert i\rvert\le W\le 300$,选出尽量多的数使和为 $T$):如果只需和 $\le T$,那么选上所有负的再贪心选正的即可(也可以从性价比角度理解,但由于所有物品价值均为 $1$,故依次选直接就是最优解)。要求 $=T$ 时,仍然考虑使得和与 $T$ 尽量接近且与最优解相差较小,于是推广贪心:在不超过 $T$ 的前提下,把能选的正的选完后如果还不够 $T$,再贪心撤回负的(可以理解成也是符合性价比原则)。这时即可同理证明贪心解与最优解相差不超过 $2W$ 个元素,可以 $\mathrm{O}(W^3)$ 多重背包。
- [THUPC 2023 初赛] 背包:设 $(v_0,c_0)$ 为性价比最高的物品。有了之前的结论,显然最优解一定塞了一堆该物品,因此只需关心 $V\bmod v_0$,或者说,问题可以转化为,对于 $i\in[0,v_0)$,可以随意选物品,其中性价比最高的物品可以选负数个,最优的答案。看起来就是个同余最短路。枚举每种物品,图可以拆成若干个环,对于一个环,易证依次松弛松两圈就够了,那就是 $\mathrm{O}(nv_0)$。
状压
状压 dp 的难点主要在两块:刻画生成过程和优化。前者没有固定方法(详见通用解题方法),后者有几个经典技巧。
第一个单独的技巧类似 meet-in-the-middle。如果转移时要考虑两个数之间的某个位运算,可以两者分别枚举一半。例子是 CSP-S 2020 初赛的最后一题。
其余的技巧都和位运算卷积有关,这里有几个经典的转移形式($\sqcup$ 表示不交并):
- $g_i=\sum_{j\sqcup k=i}f_jg_k$:这个是经典的半在线子集卷积,写成集合幂级数就是 $(1-f)^{-1}$。可以直接套用普通子集卷积的变换,然后每一位的占位多项式进行半在线卷积。仍然是 $\mathrm{O}(n^22^n)$。
- $g_i=T_i\left(\sum_{j\sqcup k=i}f_jg_k\right)$:也就是 [WC2018] 州区划分。这时可以按照 $\lvert i\rvert$ 从小到大处理(同样 popcount 的内部的 $i$ 互不影响)。也就是逐一确定所有位的占位多项式的某一项的系数。每次要先 IFMT 再 FMT,仍然是 $\mathrm{O}(n^22^n)$。
- $g_i=\sum_{j\sqcup k=i,h(j)=h(i)}f_jg_k$:也就是 USACO22FEBGoldT1。这里 $h(j)=h(i)$ 意思是 $j$ 的最高位和 $i$ 的最高位要相同。可以理解成全集的无序划分,因此写成集合幂级数就是 $\mathrm{e}^f$,因此可以直接对每一位的占位多项式求 $\exp$。第二种是按 $h(i)$ 从小到大处理,每次是一个子集卷积,时间复杂度也是 $\mathrm{O}\left(\sum t^22^t\right)=\mathrm{O}(n^22^n)$。
- $g_i=T_i\left(\sum_{j\subset i}g_j\right)$:也就是 USACO23FEBPlatinumT2。一种直观的思路是按最高位 01 分治,同时维护子集和数组。求完左边后更新右边,求完右边后更新子集和。另一种更加本质的思路是,考虑如何外层从小到大循环下标,求出子集和。为了防止计重,对于下标 $i$,考虑贡献它的 $j$ 与它最高的不同的位。那所求的就是形如 $s_{i,k}$ 表示第 $k$ 位及以上与 $i$ 相同,低于 $k$ 位的部分是 $i$ 的子集的所有 $j$ 的 $g_j$。这两种都可以 $\mathrm{O}(n2^n)$,它们本质上是相同的(第一种将第二种的子集和数组压缩成一维了)。
一个小技巧是多次位运算卷积可以把 DFT 过的数组放着,最后再 IDFT 回来,能省个 $n$。另外,$(\max,+)$ 位运算卷积应该只能做到 $\mathrm{O}(3^n)$,可以用 Karatsuba 的思路。
进一步的扩展详见浅谈集合幂级数和 EI 的 21 年集训队论文。
关于 DFT 和类 Karatsuba 算法的设计详见 LCA 的 18 年集训队论文、梁晏成的 18 年集训队论文、hehezhou 的 22 年集训队论文。
例
- [UCup2Stage4] I. Interval Addition:问题可以转化成将和为 $0$ 的数划分成尽量多的集合,使每个集合和均为 $0$。令 $t_i$ 表示集合 $i$ 内的和是否为 $0$,初步来看转移为 $f_i=\max_{j\sqcup k=i}\{t_j(f_k+1)\}$,是一个无法处理的半在线 $\max$ 子集卷积,但由于 $f_i$ 也只有在 $t_i=1$ 时有效,结合相关性质,可以直接化成 $f_i=\max_{j\subset i}\{f_j\}+t_i$,$\mathrm{O}(n2^n)$ 解决。
- [互测 2022] 整数:每一轮转移,相当于 dp 数组和允许选数的桶数组的一个复杂位运算卷积,且每一位的位运算不同,这取决于每个 $a_i$ 当前位的值。有两种运算,如果某个 $a_i$ 当前位为 $0$,那么桶数组这一位作后缀和即可转化为点积,否则相当于一个 and 卷积。
概率 & 期望
概率或期望 dp 有一个很经典的困惑是,为什么设计 dp 状态必须是“当前状态到达终止状态”的概率或期望,而不能是“从初始状态到当前状态”?
这个问题的根源在于没有澄清 dp 的对象,而普通的计数 dp 是可以设计“从初始状态到当前状态”的 dp 含义的,这就导致初学者会习惯性地类推到概率或期望 dp,但这时转移是要乘概率的,这会导致转移意义与状态意义不符。
首先,基于的模型仍然是 dfa,只不过转移边上带了个概率,dp 的本质还是统计所有路径。先假定 dfa 无环。概率 dp 如果设计“从初始状态到当前状态”其实是对的(设为 $f_i$),但是期望 dp 会有歧义:例如,设 $g_i$ 表示到达状态 $i$ 的期望步数,问题是初始状态可能不经过 $i$ 就到达终止状态。那 $g_i$ 到底表示的是一个条件期望(已知到达 $i$,这时期望的步数),还是前者乘上到达 $i$ 的概率(即所有初始状态到 $i$ 的路径的【长度乘概率积】的和)呢?
设某个前驱状态为 $j$。如果 $g_i$ 是前者,那么 $j\to i$ 转移不应乘这条边的概率(记为 $p_{j,i}$),而应该乘”$j\to i$ 在所有转移到 $i$ 的情况中占的比例,即 $P(\text{是}j\to i\mid\text{到了}i)$“,而这个玩意只能由 $\dfrac{f_jp_{j,i}}{f_i}=\dfrac{f_jp_{j,i}}{\sum_k f_kp_{k,i}}$ 得到。如果 $g_i$ 是后者,那么转移加的常数就不是 $1$,而是 $f_i$。也就是说,无论如何都要同时计算 $f$。
dfa 有环时,尽管转移类似,但是由于可能会多次到达状态 $i$,故状态的原定义出现歧义,只能改成”所有以当前状态为终点的路径的概率积和或期望和“(路径可能有无限条,但只需和收敛即可),而这个东西没有好的组合意义(甚至在概率 dp 里这个概率和可能 $>1$),就更难思考了。
总之,硬要这样设计也不是不行,但如果设计成“当前状态到达终止状态”就可以避免这些问题,从而比较简洁地直接转移。这主要是因为除了不合法情况外一定会到终止状态且立即终止(废话)。
关于概率或期望 dp 的技巧很少,有一个是某些计数问题题可以通过转成求概率或期望来简化转移公式,例如排列部分例 1~3。例 1&2 的换元形式的组合意义就是概率 dp,例 3 这类对于某些满足条件的结构的某个量计数的题,直接 dp 需要记方案数和总和,如果化成期望 dp,这个方案数就直接变成恒为 $1$ 的概率了,就只需记一个。另外一个好处是可以忽略结构中对状态没有影响的元素,直接找下一个有用的元素。
期望 dp 的一个推广是鞅的停时定理的应用,主要用于计算多结构集合和多终止状态的随机过程的期望步数。这里就不深入了。
例
CF1392H:(解 1)令一轮表示两次打乱间的所有操作。$f_{i,j}$ 表示剩余 $i$ 种牌没抽中过,当前轮还剩 $j$ 张牌,期望的剩余抽牌次数,转移很简单。题解区有些神仙直接通过这个利用待定系数法推出了正解。
(解 2)$f_i$ 表示剩余 $i$ 种牌没抽中过(当前在轮与轮之间),期望的剩余抽牌次数。这个玩意相当于解 1 的断点转移形式,可以经过数小时的推导,利用组合恒等式和换元得到正确的线性公式。
(解 3)涉及到处理期望的技巧:
$$
E[\text{抽牌数}]=\sum_{i}P(\text{轮数}\ge i)E[\text{第}i\text{轮抽牌数}\mid\text{轮数}\ge i]=E[\text{轮数}]E[\text{单轮抽牌数}]
$$
注:这个东西不大符合直觉的原因是,如果恰好在第 $i$ 轮终止,那么这轮的期望抽牌数确实不是不带任何条件时的期望单轮抽牌数。但是这里是轮数 $\ge i$,也就是说只要进入了第 $i$ 轮就算进,也就是第 $i$ 轮的所有情况都是等概率的。或者也可以从树状图的角度理解。
其中 $E[\text{单轮抽牌数}]=n\cdot P(\text{某张牌在所有joker之前})+1=n/(m+1)+1$。$E[\text{轮数}]$ 的计算有两种简单的思路:一是 min-max 容斥:
$$
\begin{aligned}
E[\text{轮数}]&=E[\max_{i=1}^n\{\text{首抽i号牌的轮数}\}]\\
&=\sum_{i=1}^n(-1)^{i+1}\binom niE[\text{首抽某i张牌中至少一张的轮数}]\\
&=\sum_{i=1}^n(-1)^{i+1}\binom ni\frac{1}{P(\text{某i张牌中至少一张在所有joker之前})}\\
&=\sum_{i=1}^n(-1)^{i+1}\binom ni\frac{m+i}{i}
\end{aligned}
$$
二是令 $f_i$ 表示剩余 $i$ 种牌没抽中过(当前在轮与轮之间),期望的剩余轮数。这里就可以用上忽略无关牌的技巧了,也就是当前抽牌只可能是未抽中的或 joker,并且抽中非 joker 后可以当场把它忽略,即 $f_i=\frac{i}{m+i}f_{i-1}+\frac{m}{m+i}(f_i+1)$,解得 $f_n=1+mH(n)$。
CF1823F:(解 1)$u\ne t$ 时 $f_u=[u=s]+\sum_{v\mid(u,v)\in E}[v\ne t]f_v/d_v$,于是以 $s$ 为根每个点的 $f_u$ 可表示为 $a\cdot f_{fa_u}+b$,然后再 dfs 一遍即可。不过这会有求 $0$ 的逆元之嫌。官方题解直接把 $f$ 的公式解出来了,我也是很被震撼。
(解 2)(来源)令 $f_e$ 表示经过有向边 $e$ 的期望次数($e$ 的反向边记作 $\overline e$),对于 $s\rightsquigarrow t$ 上的正向边,$f_e=f_{\overline e}+1$,不在该路径上的边 $f_e=f_{\overline e}$,另外一个点的所有出边的 $f$ 相等,递推即可。这个做法洞察到了更有效的数量关系。
CF1437F:先排序。为了更好地理解计数转概率的优点,这里给出这题的四种 dp 方式。记 $\#_I$ 表示大小在区间 $I$ 内的 $a_i$ 数量。
$f_i$ 表示从后往前确定,当前在 $a_i$,$>a_i/2$ 的部分的方案数。这里使用插入法,枚举下一个峰值 $a_j$,将 $(a_i/2,a_j/2]$ 部分加入 $a_j$ 后面:
$$
f_i=\sum_{a_j\ge 2a_i}f_j\cdot(\#_{(a_i/2,+\infty)}-1)^{\underline{\#_{(a_i/2,a_j/2]}-1}}
$$
令 $g_i=f_i/#_{(a_i/2,+\infty)}$ 即可后缀和优化。
$g_i$ 表示剩余 $>a_i/2$ 部分待确定,当前结尾为 $a_i$,合法的概率。枚举在只考虑 $>a_i/2$ 部分时,$a_i$ 后面一个数 $a_j$,$(a_i/2,a_j/2]$ 必须在 $a_j$ 后面,相当于 $a_j$ 是剩余部分开头:
$$
g_i=\sum_{a_j\ge 2a_i}\frac{g_j}{\#_{(a_i/2,+\infty)}-1}
$$
这个 $g$ 就是 1 中的 $g$。
$f_i$ 表示从前往后确定,当前在 $a_i$,$\le a_i/2$ 的部分的方案数。这里使用预定法,枚举上一个峰值 $a_j$,第一个空位放 $a_i$,后面加入 $(a_j/2,a_i/2]$ 部分:
$$
f_i=\sum_{2a_j\le a_i}f_j\cdot(\#_{(a_j/2,+\infty)}-2)^{\underline{\#_{(a_j/2,a_i/2]}-1}}
$$
令 $g_i=f_i\cdot#_{(a_i/2,+\infty)}!$ 即可前缀和优化。
$g_i$ 表示剩余 $\le a_i/2$ 部分待确定,当前开头为 $a_i$,合法的概率。枚举上一个峰值 $a_j$,$(a_j/2,a_i/2]$ 必须在 $a_i$ 后面,相当于 $(a_i/2,+\infty)$ 已确定并以 $a_i$ 为开头,现在和未确定的 $(a_j/2,a_i/2]$ 部分混合,要求开头是 $a_j$,并且第二个是 $a_j$:
$$
g_i=\sum_{2a_j\le a_i}g_j\cdot\frac{\#_{(a_i/2,+\infty)}}{\#_{(a_j/2,+\infty)}^{\underline{2}}}
$$
这个 $g$ 就是 3 中的 $g$。
[THUPC 2023 初赛] 公平合作:这题很好地说明了,概率 dp 两种状态定义方式其实是通的。设先手倒入 $x$,后手倒入 $y$, $m=\max a_i$,那么 $x,y>L-m$,目的是求每种可能的 $x$,后手的最优胜率 $f_x$。
(解 1)按一般的思路,$g_i$ 表示先手目前倒了 $i$ 时的最优胜率,则 $g_i=\max\left(1-f_i,\sum_jg_{i+a_j}/n\right)$。对于 $i\le L-m$,一定取后者,是一个线性递推。对于每个 $i$ 求 $f_i$,后手策略一定是 $y\le i$ 时继续随机,$y>i$ 时停止,因此仍然是个线性递推。这些递推(包括 $g$)的公式均相同,待求远处项位置也相近(至多差 $m$),只是初值不同,因此利用倍增求线性递推数列一项的技巧,可以 $m^2\log L$ 求得一个,然后 $m^2$ 推出其他。
(解 2)计算某个 $f_i$ 是一个单起点多终点的 DAG 上游走问题,官解是令 $f'_{i,j}$ 表示从 $x=i$ 时,后手从 $0$ 开始,最终停在 $j>i$ 的概率(必须是在 $>i$ 是最先到 $j$,否则会计重)。$f'_{i}\to f'_{i+1}$ 就转移一下 $f'_{i,i+1}$ 即可,计算 $f'_{L-m}$ 也可以线性递推。计算答案时也是考虑 $x$ 最终到几,$ans=\sum_{i>L-m}f'_{L-m,i}g_i$。这个思路初看不大自然,但它其实就是正着定义状态的版本。
数位
一般的数位 dp 无非就是在进位和压上界的处理上变个形,没什么可多说。
关于全体 ${}+x$ 的最优化问题(例如 CF778E、ARC153D),考虑逐位 dp,记录进位的分界线。如果当前确定的是低 $i$ 位,那一定是所有数按低 $i$ 位排序后的一个后缀进位。转移时先基数排序,再枚举进位分解,得到下一位每种数占的区间,再枚举下一位。
另一个值得注意的模型是,考虑函数 $f(S)=\{\lfloor x/2\rfloor,\lceil x/2\rceil\mid x\in S\}$,那么 $f^{(i)}(\{x\})$ 的大小至多为 $2$。这是因为 $\lfloor\lfloor x/a\rfloor/b\rfloor=\lfloor x/(ab)\rfloor$,故 $f^{(i)}(\{x\})=\{\lfloor x/2^i\rfloor,\lceil x/2^i\rceil\}$。如果考虑的是可重集合,那么 $f^{(i)}(\{x\})$ 中恰有 $2^i-x\bmod 2^i$ 个 $\lfloor x/2^i\rfloor$。这可以通过 $\lceil x/2\rceil=\lfloor (x+1)/2\rfloor$ 推得。
例
CF1815D:$m\ge 3$ 时显然可取到所有 $\le n$ 且与 $n$ 奇偶性相同的数。$m=2$ 时考虑逐位 dp。如果 $n$ 最低位为 $1$,那么只有一种转移,否则可能两个数最低位均取 $0/1$,且由于这两种情况下剩余部分 $n$ 的奇偶性不同,故可取得的异或值一定不交,因此转移形如 $f_n=f_{n/2}+f_{n/2-1}$。无论如何,有效状态至多 $2\log_2 n$ 个。可以用 map,也可以将状态理解成是否进位,开一维 $0/1$。
AGC064C:暴力是把二进制表示倒过来建 trie 树,$f_u=f_{{ls}_u}\operatorname{nand}f_{{rs}_u}$。建树的过程是如果当前要插入 $[l,r]$,就往左子树插入 $[\lceil l/2\rceil,\lfloor r/2\rfloor]$,往右子树插入 $[\lceil(l-1)/2\rceil,\lfloor(r-1)/2\rfloor]$,这立即启发我考虑,同一层内的不同构的子树数量少。确实是这样的:
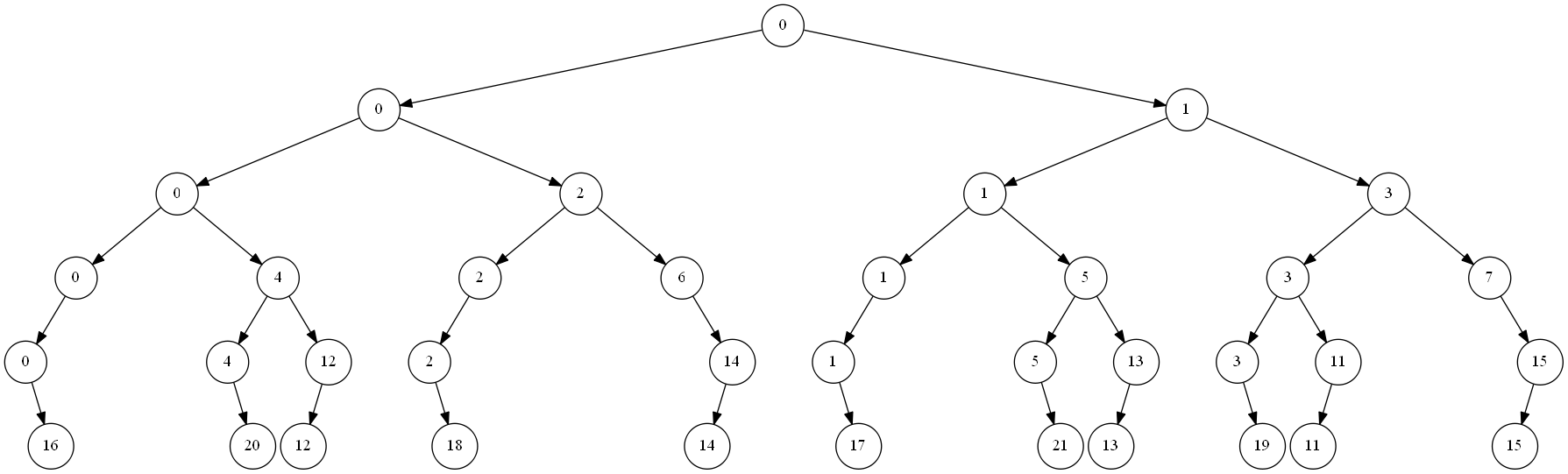
这是 $[11,21]$ 的 trie 树,发现每一层至多 $3$ 种子树。进一步地,对于第 $i$ 层(从 $0$ 开始)的 $x$ 号(编号定义为从根到它的路径的 01 序列反过来对应的二进制数)节点,$[l,r]$ 在它上面生成的子树为 $\left[\lceil(l-x)/2^i\rceil,\lfloor(r-x)/2^i\rfloor\right]$,也就是会将 $x$ 可以取的 $[0,2^i)$ 切成至多三段。那么 $n$ 个区间至多切 $2n+1$ 段。总体来说,逐层枚举,使用基数排序和指针扫描可以做到一个 $\log$。
树形
树形 dp 的套路基本上已经出烂了,可参考任轩笛的 18 年集训队论文和张哲宇的 19 年集训队论文。
设计思路上基本就是考虑加一条边和合并两个儿子,把状态和转移定出来。比较初级的技巧包括换根 dp、多儿子选择时的反悔技巧、树上背包。其中树上背包如果强制大小与 $k$ 取 $\min$ 的话时间是 $\mathrm{O}(nk)$ 的,证明见下。
还有一种 dp 方式是在 dfs 序上跳。
例
- CF1097G:考虑 $\lvert E\rvert^k$ 等于选出虚树中边的有序可重 $k$ 元组数量,这就可以树上背包,合并用组合数。对于底部选出的边,子树里至少选一个;如果有一条最顶部的边,那外部至少选一个。稍加讨论即可。$\mathrm{O}(nk)$ 的证明可以考虑模仿一种树分块:子树 $siz\le k$ 的点称为小点,剩余称为大点。每个极大的小点子树都是 $\mathrm{O}(siz^2)$,由均值不等式至多 $\mathrm{O}(nk)$。小点顶部转移给大点是 $\mathrm{O}(siz\cdot k)$,共 $\mathrm{O}(nk)$。大点之间,两个大点合并为 $\mathrm{O}(k^2)$,合并共发生 $\mathrm{O}(n/k)$ 次,也是 $\mathrm{O}(nk)$。
- [APIO2021] 封闭道路=CF1119F:由于 $\sum_k\sum_u[deg_u\ge k]=\sum_udeg_u=n$,故可以暴力做。对于一个点,有一些 $deg\ge k$ 的儿子,还有一些其他边。使用反悔技巧,断儿子的代价为 $f_{v,1}-f_{v,0}$。这些其他边不能全部排序,必须只取最小的 $deg_u-k$ 个来归并,从大到小枚举 $k$,用链表维护即可。
其他. CF868E
区间
这部分不是指区间 dp,而是某些给定若干区间然后选的问题。这类问题较罕见,我尚未总结出较好的技巧,几个初步的处理方式是按某个端点排序,以及处理掉一些区间使得左右端点同时递增或只有包含和相离情况,典型的例子(非 dp 题)分别是 CF1774G 和 CF319E。
例
CF1832F:对于一个人工区间,所有可能的自动区间与它配合导致的失守时间是一个斜率一次为 $1,0,-1$ 的分段函数,因此原问题是按 $(l_i+r_i)/2$ 排序后分段贡献,这就将二维化成一维,更好处理了。求一段共用一个自动区间的最优解是容易平方的,因为代价是凸的,离散化一下走指针即可。剩下的就是四边形不等式的形式 2,证一下四边形不等式即可。
CF1250D:称不高兴的科学家为全同区间,容易发现全同区间形成一些内部同色的不交段。考虑按右端点排序后 dp,那致命的问题是在一个区间后面的区间可能包含它,无法确定后者是否全同。按左端点排序则能避免这个问题,状态只能记目前最后一个全同区间(否则也会信息爆炸),我们将会看到这个状态的隐含条件(与当前区间相交的区间均与它同色)十分重要。记区间为 $I_{1\cdots n}$。若 $I_{i+1}\subseteq I_i$,则继续往后看,注意不能转移到 $i+1$,否则会丢隐含信息。若走到了一个不是包含但有交的 $I_j$,如果决策它也是全同,那就无虑地转移过去;如果不这样决策,就继续扫,直到不交,后面就任选一个开启新的全同段。这个是 2D/1D 的,我感觉可以再优化,但不会。
像这种区间问题就感觉很奇怪,一个合理的状态能给出极好的无关性。
数学方法
GF 相关详见这里。
这里讲些题外话。一些具体的数学处理方法详见下一章。
我们无法找到一个通用的方法,判断解一道(计数)题设计 dp 和直接推式子孰优孰劣。推式子往往需要更透彻的对模型的分析(从而转化成能只用乘法原理描述的结构),但可以利用各种数学工具得到不依赖于组合意义的、更本质的解法,因此我们往往发现推式子后复杂度更优,例如 USACO21DECPlatinumT3,以及一些经典递推序列的通项等等。但情况也不全是这样,例如 [联合省选 2023] 染色数组 的第一问有一个 $\mathrm{O}(nm^2)$ 的 dp,但推式子(应该?)只能做到 $\mathrm{O}(n^3m)$。这两者的分界到底是什么?这是一个让我很困惑的问题。
在 dp 题中,数学方法往往用于引导一些难以赋予组合意义的优化,例如 GF 等等。一些可以机械化的优化包括:矩乘相关(行列式、特征多项式、对角化等)、常系数线性递推、整式递推(详见 zzq 的 19 年集训队论文)。
一维的递推数列已经基本上能解决了,但是二维的我目前找到这篇和这篇,或许依次处理两个方向即可?那我的互测题能否代数推导保平安呢?能否线性呢?
另外一个方向是,常系数线性递推的快速幂+多项式取模方法意味着 $P(x)/Q(x)$ 的远处项可以快速求,于是可导出 $\ln P(x)$ 的远处项也可以快速求。整式递推的点值平移方法给出了一类生成函数的远处项的根号做法。那其他的特殊情况的远处项呢?例如 $\sqrt{P(x)}$ 和 $\mathrm{e}^{P(x)}$?是不是扯得太远了……
如果您对这些方面有了解,请不吝赐教。
通用的解题方法
思考一道 dp 题的过程可以归纳为如下四步:
- 分析模型性质,简化模型,揭开模型“真面目”;
- 处理模型,找到可以用 dp 解决的对象;
- 明确转化后的问题,设计 dp 方式;
- 优化 dp。
其中相邻两步之间没有明确的分界。同时思考过程并不一定是依次做这四个步骤就行了,可能在第四步时会返回到前三步,重新分析组合意义,反复寻找更优的 dp 方式。
接下来就逐个讲解。
第一步 分析性质
与其说这是 dp 的第一步,不如说所有题第一步都要做类似的工作。这一步主要是在不主动改变或加强模型的情况下,分析模型的性质,从而转化模型,使其更容易被把握。
第一、二步的核心都是减少总体(静态)的模型可能性,区别在于,第一步是基于题目条件作有充分性的推导,明确在题目条件下未知部分的哪些情况是可能的,如何用更简单的命题描述;而第二步的目的性更强,会为了使结构能被 dp,更加激进地主动转化模型,改变原有的模型结构和要素组织方式,寻找一个具体的刻画,组织所有可能的解。
这一步和贪心或无算法题的分析过程较类似,具体技巧千变万化,这里就简单讲一下基本的方法。
在这一步中,主要思考以下内容:
寻找可以直接从题目条件导出,或与题目条件等价的条件;
模拟(包括打表)小样例、特殊样例找到简化的方向和规律;
想象某个最终解,利用(广义的)调整法排除可能性,即“具有这样特征的解一定包含最优解”。更具体的技巧可以参考这里。这个思考主要用于最优化,但是其他类型的模型如果条件较复杂,交织在一起,也可以通过想象解,并调整或排除使之切合题目条件,得到对解的结构的直观认知。画非具体样例式的模型图是很有用的。
另外,如果解是一个过程,有时倒推一些必要的东西会比较容易。
联想一些与题目条件相关或类似的模型,尝试套用。
具体来说,主要会得到以下两类观察:
- 条件或模型的等价但更适合处理的转述。有的题有着非常晦涩的条件,通过分析或换角度描述,可以使它更容易处理。
- 结构、情况、过程的简化。这种简化不仅仅包含贪心性或排除性的简化,也包含对模型更深入的理解,将结构更明确、更简单地描述出来。
算了比较难描述,还是看一些具体例子吧……
例
[联合省选 2023] 染色数组:这题显然要将“划分成增减序列至少有两种方案”转化成更直观的条件,然后再 dp 或推式子。转化的分析详见题解区。
[NOI2016] 国王饮水记:如果任选子集,那完全无法处理。考虑挖掘性质:① $h_1$ 一定递增;每次选一定包含 $h_1$;除 $h_1$ 以外,其他的一定至多选一次;② 每次选的 $h$ 中 $\max$ 一定 $\le$ 下一次选的 $h$ 中 $\min$;③ 将 $h_{2\cdots n}$ 排序,每次一定选连续一段,且相邻两次选的之间一定无空隙,且最后一次一定选到末尾。这样分析完之后 dp 自然就出来了。后面进一步的除决策单调性以外的优化其实也是基于对原问题模型的分析(长度不为 $1$ 的区间很少)。
注:① 得三个子性质一起归纳,每次调整最后一个不满足性质的,不然是无法严谨证明的;②③ 可以直接反证法+调整。参考官方题解。
CF1368H1:题目是以最大流的语言给出的,但如果只从最大流或最小割的角度来看是无法简化结构的,必须要考虑对偶图最短路——参考 [CSP-S 2021] 交通规划,模型等价于所有红蓝交替处作为端点,两两匹配(奇偶性必须不同)求最短路之和。本题中 $n,m$ 很大,但由于边权都是 $1$,故只需保证路径长等于曼哈顿距离即可。可以将矩形邻边上的匹配贴到边界上,对边上的匹配拉直(只会有一组对边上匹配),简化了结构。但这样的匹配还无法 dp,必须将该性质用最小割的语言描述——每行或每列颜色均相同,然后即可线性 dp。
这题是非常典型的不断转化等价模型并观察,从而找到突破性质的题。
CF906C:注意到选的点集导出子图一定是连通的(否则选的点之间会无边),同时易证选这个操作其实是无序的。这两个观察使模型清晰了很多。问题就转化成选一些连通的点使得它们的邻点并集包含所有未选点。按 bfs 的顺序状压 dp 即可。
CF1503E:考虑蓝色的区间从上到下的移动情况,如果相邻两行不交则称为“断”。发现至多断一次,即蓝色形成 $1/2$ 个连通块,否则一列中的黄色会被割裂。如果是两个连通块,则一定分别是单峰的,否则黄色部分一定是两个单峰的连通块。这题可以直接推式子算。
USACO22DECGoldT1:想象最终选的朋友,发现 $B$ 一定花给这些朋友按 $X$ 排序后的前缀。于是按 $X$ 排序后背包,一定是先花 $B$ 再花 $A$,三维 dp 转成两个两维 dp。
第二步 处理模型
(第一、二步往往是连续进行的,尤其是一些没有固定形式的转化和抽象过程,很难说清属于哪一步。)
这一步中应当完成对静态模型的处理,将其彻底转化成可以 dp 的模型,并用更本质的语言去描述它,用更有效的角度去看待它,并在最后进行汇总。注意,这里的“静态”是与第三步的 dp 生成过程(局部)形成对照,并不是说模型本身必须是静态的,而是从一个整体的角度看待模型。
您可能还不是很明白。可以类比推式子题来理解——当我拿到一个计数模型,一般不能直接写出式子,而是要考虑:要先转化等价模型吗?是否要套容斥或反演?该对模型的哪个部分计数,这些部分如何组织?枚举什么量,枚举顺序如何?等等。这些问题的答案共同构成了处理一个模型的具体思路,然后再写式子。
要寻找处理模型的方法,固然对于某些有特定特征的题可以套用一些转化技巧,接下来也会讲;这里我先提出一个通用的思考方法:考虑模型的“要素”。要素,一般是模型结构的组成部分、相关量或维度。一个模型包含多个要素,要素之间的关系就是题目条件和描述,以及导出的性质。通过改变(增删、合并、拆分、等价转述)要素,调整这些要素的主次关系、自变量与因变量关系(包括无关、守恒等特殊关系)、组织顺序(例如有两个维度,先看哪个,或者时光倒流等)、枚举顺序等,得到一个新的看待模型的方式。在新的模型描述下,所有解应与原模型的所有解形成一个映射(双射)。至于如何判断转化是否有用,那就还是从信息量(不确定性)的角度考虑。
一个最简单的例子就是上文中排列部分前两题,原模型是一个排列,但排列中各个元素的效果不同。现在只关心其贪心单调子序列这一部分要素,剩余部分通过组合数,也就是数学方法消除掉。
例
[CSP-J 2019] 纪念品:这题的关键在于拆分“纪念品的持有时间区间”这一要素,将它拆成相邻两天之间是否买进卖出,这样各天之间的决策就无关了,逐天背包即可。
CF1580D:这题难处理的是一堆区间 $\min$ 这个东西,考虑搬到笛卡尔树上,全局 $\min$ 的贡献就变成了左右选的数量之积,往下递归形式是一样的,dp 状态自然就出来了,树上背包即可。这题就是寻找一个更好的结构,转述要素(注意和第一步中的套用模型是不同的,这里考虑笛卡尔树不是为了进一步发掘性质,而是直接尝试 dp 了)。
AGC056E:先固定没吃的老鼠。从时间维看该过程是没法多项式时间的。考虑一起看所有奶酪的轨迹(轨迹包含投掷初始位,多次尝试被吃和最终被吃三个部分),注意到如果有多块奶酪经过一只老鼠,它们后续的轨迹之间是可以交换的,也就是说只需保证同一块奶酪按顺序依次尝试被吃即可,多块奶酪之间的尝试是无序的,因此就可以从下标维来看轨迹,dp 记录当前已确定的奶酪数 $x$,每次以 $1-1/2^x$ 的概率吃。然后问题就在于它这个过程是无限的,但是只要所有奶酪确定了,就可以用数学方法算剩下的无限圈了。题解区第一篇的考虑方法很有意思,再将问题转化回逐个奶酪移动,这样概率就变成了一个乘积式。
CF1842H:初始的题目模型无法处理,考虑将所有 $x_i$ 减 $0.5$ 后转化成一堆 $x_i\;\boxed{>}\;{-x_j}$ 形式的偏序关系。想象数轴上这些 $\pm x_i$ 的分布,$O$ 的两侧是对称的两半,直接 dp 一半发现得记已确定的变量和它的正负情况,那就得 $3^n$。但细看发现很多状态不合法,因为例如 $x_i+x_j<0$,那么 $x_i$ 与 $x_j$ 中绝对值大的一方必须 $<0$,因此只要按绝对值大小 dp,就只有那些最先(或最后)(相对于它所受约束的其他相关变量)确定的变量可能正负不定,但这些正负不定是无所谓的,而其他变量的正负都可以通过当前的已确定 bitmask 推得。从拓扑序角度也可以得到符合直觉的解释。
这题不仅考察对模型的处理,还要求转化后不遗忘原模型的对称性质,再次回到第一步进行性质分析。
补充一下,并不是所有对模型的处理都要进行转化,导致 dp 困难的往往是对模型的理解不够本质。所以不要急于改变要素,要先看清所有要素。
例
USACO21DECPlatinumT2:显然配对端点同时递增。$T=1$ 利用扩大可行域技巧即可。$T=2$ 时,我当时执意考虑按从小到大扫一类牛的顺序 dp,这样直接做得记录当前对以及上一个(或两个)未配对牛以保证极大性,如果要避免第三维就得在出现不选时断点转移到下一个不必要考虑之前未配对牛的状态,但这样中间的讨论就炸飞了。我犯的错误是没有全局观,应当同时观察两类,这时不选的牛的品种随坐标增加在两种之间交替,且交替处间隔多余 $K$。因此得到了一个新的方案:记录当前两类待配对的下标,以及当前允许不选的品种。如果要更换品种就进行一段选满的断点转移,合法性可以预处理。
其实可以发现,后面这种观察方式说的其实都是废话,也没有转化模型,但是若不这么考虑就是没法 dp。所以角度很重要。
CF1299D:首先要知道 dfs 树上所有返祖边对应环构成所有可能回路经过奇数次的边(若干不交简单环)的异或空间的一组基,相应地只考虑边权也是一样。因此可以把根伸出的各块每个视作一组异或空间。这里要将 $5$ 位异或空间及其合并运算一起视作一个交换半群(元素个数为 $374$,详见 A006116),再分讨根周围的块:要么与根连一条边,要么与根形成三元环,然后就做一个类似背包的东西即可。
这题的关键在于把线性基合并抽象成代数运算。
然后是一些特定的转化技巧。
外套方法
这类方法直接作用于变量,主要包括枚举、二分(仅限最优化)和容斥(仅限计数)。二分主要包括二分答案和 WQS 二分(入门、进阶),容斥其实就是各类反演(炫酷反演魔术,还可以参考周子衡的 23 年集训队论文),不过建议推导时不要丢掉组合意义,不然可能会漏性质或失去动机。枚举和二分答案的实质就是减少不确定性,WQS 二分和容斥的实质就是去除或弱化变量限制条件。
例
CF1784E:只考虑 $\Delta$ 表示 A 赢减 B 赢(经典套路)。这题大致的模型是,把循环节理解成一个黑盒,循环连接处只需提供少量信息即可确定整体的 $\Delta$。具体的接口抽象方式有两种:一种是考虑每个开头忽略 $0\sim 2$ 个后,结尾还需在下一次循环中取几个。这个必须要枚举开头两个字符。另一种是将比赛过程抽象成四个点的 dfa,考虑开头时的状态和结尾时的状态。
这里就出问题了,将每种情况 $\Delta$ 记在状态里,势必会导致 $n$ 的较大次方(且事实上即使利用各情况的 $\Delta$ 间关系也不足以将次方缩得足够小)。而反复循环的接口处状态实际上构成基环树形态,结合题目所求,只需关注基环部分状态的 $\sum\Delta_s$。那就枚举基环所包含的状态集合,这样 dp 只用记状态之间的转移关系用于吻合枚举的情况,时间复杂度大常数 $\mathrm{O}(n^2)$。
[IOI2016] Aliens:可以将兴趣点转化成区间。对于不限制 $k$ 的情况,首先有一个 $\mathrm{O}(m^2)$ 的 dp,似乎不大能优化。考虑将 dp 对象转为区间(按右端点排序),或者发现只有右端点位置的 dp 值有用。列出 dp 方程发现可以四边形不等式优化或斜率优化。另有性质:答案关于 $k$ 下凸(用四边形不等式证),WQS 二分即可。细节详见官方题解。
CF1707D:直接 dp 得记每个时刻是否选真子集,爆炸了。令 $f_i$ 表示 $i$ 次内消得只剩根的,允许单次不变的方案数,$g_i$ 表示原答案,那么 $f_i=\sum_{j=1}^i\binom ijg_j\Rightarrow g_i=\sum_{j=1}^i(-1)^{i-j}\binom ijf_j$。$f$ 可以通过最自然地 dp 子树 $i$ 在 $j$ 步以内消光的方案数得到。转移时枚举根何时消去,消去后仍允许一个子树剩余。方程的主要部分形如 $f_{u,i}=\sum_{v}f_{v,i}\left(\sum_{j\le i}\prod_{w\ne v}f_{w,j}\right)$,可以前后缀积优化。
(相互再归的鹅妈妈):不容斥没法搞。容斥后的计数有两个思路,一个是无序(强制不降),一个是有序。无序得状压;有序可以只记压上界的数量,进一步考虑到一旦有不压上界的数就选出一个用于凑 $0$,从而用公式计算,应该可以做到 $\mathrm{O}(m)$,但是容斥起来麻烦些。一种思路是直接对于两两不相等的条件容斥,枚举钦定相等形成的等价类,设大小 $a_{1\cdots k}$,容斥系数为 $\prod f(a_i)$,$f(n)$ 表示所有 $n$ 点连通图的 $(-1)^{\lvert E\rvert}$ 之和,有 $[n=1]=\sum_{x_1+\cdots+x_m=n}n!/(m!\prod x_i!)\cdot\prod f(x_i)=[x^n/n!]\mathrm{e}^{\operatorname{EGF}(f)}$,从而 $f(n)=[x^n/n!]\ln(1+x)=(-1)^{n-1}(n-1)!$。这部分理论上可以做到 $\mathrm{O}(k\log k)$。
[互测 2023] Permutation Counting 2:欧拉数的和式推导可谓非常经典——钦定连续上升段,段间无法保证下降,就用二项式反演容斥:钦定 $i$ 个上升段的情况,会将恰好有 $j$ 个上升段的情况计入 $\binom{n-j}{i-j}$ 次。具体推导就不写了。那这道题这样容斥后就转化成,求 $q_{1\cdots n}$ 数量,满足 $1\le q_k\le i$,$1\sim i$ 中每个数至少出现一次,且 $q_k\le q_{k+1}$ 恰好有 $j$ 个。 “每个数都出现”这一条件可以套容斥,规定上升数可以再一次容斥,内层就变成了简单的非空不降序列。最内层的容斥可以推出一个线性的类似欧拉数的求和式,再依次进行剩余两层容斥就行,$\mathrm{O}(n^3)$。
这里补充一下。个人感觉二项式反演很费脑,考试时建议把正向的式子写出来然后直接套结论(如果形式不对就换元),但平时还是尽量在脑中过一遍组合意义,还是很精妙的。
其他. +CF663D、+CF1799G、判定型计数里的一些题、+[NOIP2018] 赛道修建、CF1322F、CF739E、CF1799F
公式变形
这个就不必解释了。
例
CF946F:(解 1)对于所有子序列,求出 $s$ 出现的次数,那实质上就是在 KMP 自动机上走,每遇到一个字符允许不走。矩乘描述即可。
(解 2)考虑交换解 1 中的两个 $\sum$,对于 $F(x)$ 中所有的子序列 $s$,设开头在 $l$,结尾在 $r$,那贡献为 $2^{l-1+n-r}$。令 $f_{i,l,r}$ 表示 $s_{l\cdots r}$ 几次作为子序列出现在 $F(i)$ 中,特殊地,若 $l=1$ 或 $r=n$,就同时算上外部的 $2$ 的次幂。
CF856C:数字 $x$ 可抽象为 $(x\bmod 11,\operatorname{len}(x)\bmod 2)$,方案中一个数的贡献取决于它所在数位的奇偶性,得考虑顺序,但无法直接 dp 排列。只能考虑先 dp 每个数所在位的奇偶性,然后再用数学方法算。$\operatorname{len}$ 为奇的恰好一半一半,偶的任意插空,先分开 dp,再合并。
USACO23OPENPlatinumT1:将子序列匹配理解成自动机上走,可以得到一个矩乘表示,但是得记 $7\times 7$ 太大了。考虑抽象成一维的表示。线段树上每个节点记录:① 每种状态经过该区间后的状态;② 每种状态经过该区间且在该区间内终止的贡献;③ 每种状态经过该区间且尚未终止(走到右端点)的贡献;④ 在该区间内起始且尚未终止(走到右端点)的新增各状态数;⑤ 在该区间内起始且在该区间内终止的贡献;⑥ 在该区间内起始且尚未终止(走到右端点)的贡献。要把区间内终止和尚未终止(走到右端点)分开来记是因为往后延伸的话会贡献多次。
以上是我考试时的做法,后来看题解发现可以只记四类信息:将 ② 和 ③ 合并成 ②${}+(n-r)\cdot{}$③,⑤ 和 ⑥ 同理。为什么我写复杂了?因为我是按题意原样做的,而合并实质上是对于每一组(区间开头,一组匹配)分开看它们的贡献,出现一组匹配后后面结尾在哪是无关的,直接乘 $n-r$ 就行。所以说对初始模型理解的细微差别可能导致实现时复杂程度的大差距。
USACO20OPENPlatinumT2:(解 1)考虑对于每一个 $p^k$ 计算有几个置换中包含至少一个长为 $p^k$ 倍数的环 $\bmod(M-1)$。令 $f_i$ 表示大小为 $i$ 时,有几个不包含。转移模仿第一类斯特林数:
$$
f_i=\sum_{p^k\nmid j}(i-1)^{\underline{j-1}}f_{i-j}
$$
由于模非质数故无法换元,但可以记前缀和每次乘 $(i-1)$。可以利用同余技巧,通过对 $i\bmod{p^k}$ 分组记和做到单次 $\mathrm{O}(n)$。
(解 2)(来源):钦定 $c$ 个长为 $p^k$ 倍数的环,是普通容斥,系数 $(-1)^{c-1}$。$f_i$ 表示钦定 $ip^k$ 个数(环数不记,直接压在一起)的和:
$$
f_i=-\sum_{j=1}^i\left(ip^k-1\right)^{\underline{jp^k-1}}f_{i-j}
$$
$$
ans\xleftarrow{\times}\operatorname{pow}\left(p,\sum_{i\ge 1}n^{\underline{n-ip^k}}f_i\right)
$$
总状态数是 $\mathrm{O}(n\log\log n)$ 的,可以用 ds 优化连乘。
[WC2021] 表达式求值:这类涉及大小关系的问题常考虑 $01$ 情况。数组逐位做,设当前 $a_{*,j}$ 排序成 $x_{1\cdots m}$,将其差分,答案转化成 $\sum_{i}(x_i-x_{i-1})[E([a_{1,j}\ge x_i],\cdots,[a_{m,j}\ge x_i])=1]$(这个套路也往往在算期望时用),这时所有叶子只有 $2^m$ 种分布情况,且 dp 可转移。
判定型计数
判定型计数问题主要指一类直接对着题目合法条件 dp 会导致同一个解被重复计入的问题(广义地说,所有计数都是判定型的,但显然这不是这里希望讨论的)。这类问题的通用处理方法有四类:转述条件(例 9&11)、钦定单射(例 1&4&5)、容斥(例 4&7)、对判定过程 dp(例 2&3&6&8&10&12)。转述条件就是将判定条件能转化成对解本身更简单的限制,然后强制直接对解 dp。钦定单射主要指对于一个合法解的多个证书,通过规定偏序关系等方式,钦定唯一一个被计入的证书,来 dp。对判定过程 dp,如果判定过程是 dp,那就是常说的 dp 套 dp。也可能是贪心等其他算法,不一定要是 01 的判定过程。有些非判定型计数问题(不易计重,但也不易直接 dp)也会用这个技术,例子都放在这里。
另外某些特殊的问题可以记录一维 $0/1$ 表示是否存在至少一个达成的方案。
remark. 钦定单射和容斥在论文中统称带权计数,注意两者的区别。例 4 不能理解成对计重容斥,因为并没有某组 $A/B$ 选择贡献了负数,用论文中的话来说就是没有 $w(y)<0$。这题的容斥只是为了保证有且仅有 $w(\text{独立区间均选}A\text{的方案})=1$。而例 7 是实打实的容斥,这题不能把 $Y$ 看作 $1\sim n$,而必须看成 $1\sim n$ 的所有子集,不然“计同时能被多个下标满足的方案数”这个事就没法解释了。当然讲的这些在实操时没必要刻意区分。
例
CF1679F:这题虽然不是判定型的,但也易计重,用到了钦定单射的思想。考虑只对每个等价类的极小元素计数,极小元素定义为,每个数字 $d_i$ 向前看,都有一段相邻的可以交换的数(然后遇到头或一个不能交换的数),这些数都要 $\le d_i$。这个极小元素是存在且唯一的,可以借助字典序这一偏序结构证明。于是可以状压 dp,记录当前位可以取的数。
CF1810G:这题也不是判定型,但是官解(解 2)用到了对判定过程 dp 的思想,故也放在这里。
(解 1)我的思路是,考虑固定前缀和的 $\max$。$f_{i,j}$ 表示 $s_i$ 将前缀最大值刷新为 $j$ 的概率,这可以通过有限制折线的经典容斥来转移:$f_{i,j}=c_{i,j}-\sum_{k
这个方法的大致思想是,直接 dp 需要记当前的和与总的 $\max$(都会变),尝试省掉一方,那就固定 $\max$。最近又去看了一下题解区,发现这篇题解虽然不是容斥,但是也同时用了“固定 $\max$”和“多个 dp 合并起来做”这两个思想,饶有趣味(如果您能给出对这类技巧更宏观的解释,请告诉我)。
(解 2)考虑寻找一个不需要记三次方状态的求最大前缀和的方法,然后对该方法 dp。一个脑洞大开的想法是,从后往前扫,只维护求最大子段和时的 now 变量(含当前位置的最大和),当 $<0$ 时丢弃,置成 $0$。
CF924F:求划分最小差只能用背包,可以证明背包只需开到 $72$,这时状态数只有 $12880$ 个。通过合并等价状态可以达到 $715$ 个。然后就是一个数位 dp,预处理 $f_{k,i,s,r}$ 表示限制差 $\le k$,$i$ 位待定,当前 dfa 上状态为 $s$,当前位至多取 $r$ 的答案,即可 $\mathrm{O}(T\log r)$ 回答。
这里用到了 dp 套 dp 中两个核心技巧:只 bfs 可能被达到的状态和合并等价状态。其中后者也是 SAM 的思想来源。两种朴素的合并方法是哈希(求出每个点向后 $C$ 层的状态,取一个合适的 $C$)和连锁合并(先合并出点编号完全相同的,再不断找新的可以合并的,缺点是有两个完全相同的环时无法缩)。
关于 $72$ 的证明与最小 dfa 的求法(Hopcroft 方法)详见徐哲安的 21 年集训队论文。
AGC061C:这题涉及两个对象的关系:$A/B$ 之间的选择以及得到的排列,多个选择可能对应同一排列。考虑计重如何发生,直觉上来说形如一个区间内没有其他端点被选(称为独立区间),然后它分别选两个端点,并且容易想到对于每个独立区间,钦定它必选 $A$。但是为了保证这样,dp 时就要记上一次选 $B$ 的位置,至少平方。考虑容斥,钦定若干错误(独立区间选 $B$)选择,它们必然不交,且由输入性质,不存在与它们都有交的区间(否则就会两头均无法选),从而,只能选一端的区间数量为与每个钦定独立区间有交的区间数之和,只需要前缀和优化即可 1D/0D。可以把这个设计理解成先钦定单射(选择的字典序尽量小,只记)再容斥,也可以理解成直接对计重容斥。
这里的钦定单射还要严谨证明正确性:如果有两个选择方案,它们的独立区间全选了 $A$,却仍然生成了相同的排列,那么按排列中的顺序,找到第一个选择得不同的区间,这个区间不能是独立区间,那么它内部被选的其他端点必然会导致两个排列不同,矛盾。
AGC056B:这题是排列映射到 $\operatorname{argmax}$ 序列。考虑计重的特征,换句话说,考虑一个 $\operatorname{argmax}$ 序列对应的所有原排列的刻画。模拟样例发现,直觉上有多个“局部最大值”,它们互不影响,那么原排列任意换这些位置的相对大小,这时会计重。将直觉严谨化,如果所有包含位置 $i$ 的区间的 $\operatorname{argmax}$ 都取到 $i$,那么可以 $p_i=n$。钦定单射,若有多个 $i$ 就取最小的,这样易证不会计重。将这些区间去掉后可以得到形式基本相同的子问题,唯一的限制的是左侧不能再出现上述的 $i'$,即规定左侧的最大值必须取在某个包含 $i$ 的区间内,即属于一个后缀。这可以做到 3D/0D。
USACO22FEBPlatinumT3:考虑如何判定一个序列 $t$ 能被原序列 $s$ 生成。$f_{i}$ 表示 $t_{1\cdots i}$ 能否被 $s_{1\cdots i}$ 生成,除了 $s$ 中的元素,$f_i$ 还依赖于 $f_{i-1},f_{i-2},f_{i-3},f_{i-4},t_{i-1},t_{i-2},t_{i-3}$。dp 套 dp 的常数不得上天?考虑对记的状态剪枝:只有 $f_{i-4}=1$ 且 $\{s_{i-3\cdots i}\}$ 合法(为四种 $2\times 2$ 之一)且 $\{t_{i-3\cdots i-1}\}\subset\{s_{i-3\cdots i}\}$ 才有必要记 $t_{i-3}$,这时只有 $24$ 种可能;否则考虑 $\{s_{i-2\cdots i+1}\}$,$\{t_{i-2\cdots i-1}\}$ 有 $12$ 种;否则 $9$ 种。我的实现是不考虑 $f_{i-*}=0$ 的剪枝,这样共有 $15\times 45=675$ 种状态。应该可以进一步缩,可能也能套用 dfa 的通用缩状态技巧(加之删去只能到达非法状态的状态),但是转移边得同时定 $s_i$ 和 $t_i$,这不如直接剪枝(还可以利用 $s_{i+1}$)。像这种判定条件由输入给定的情况建议直接结合组合意义缩状态。
remark. 这题也可以跑缩 DFA,结果也很优秀,详见论文,劲爆代码。
[NOI2021] 机器人游戏:这题求的是有几组 $(\{X_i\},\{Y_i\})$ 能被至少一个初始位置 $p$ 生成,那就容斥,枚举初始位置的集合,会得到每一个格子的方案数,暴搜或 dp 即可。后续分两类处理与 dp 无关,略。
同样使用容斥处理计重的还有 [十二省联考 2019] 希望,利用树的连通子图点减边 $=1$ 的特性。
[互测 2023] 栞:考虑求 $f_k(p)$ 的方法,存在一个简单的贪心——容易证明 $f_{k}(p)\le f_{k+1}(p)$,因此每次对于所有可能的第一段,选择排序后的最小者(如果 $s$ 是 $t$ 的真前缀则 $s
但是延后决策毕竟要记一个下界,还是比较麻烦,考虑结合条件进一步分析。设 $q$ 的第一个上升段是 $q_{1\cdots l}$,那么 $p_l$ 处一定会分段。设进行以 $l$ 结尾的这一段的决策时,最右可选为 $p_{l'}$,如果 $l'=l$ 那就没事了。否则 $p_{l+1\cdots l'}$ 都得大于 $q_l$,且下一段最右可选为 $p_{l'+1}$,又由于 $q_{l}>q_{l+1}$,故 $p_{l'+1}$ 必须 $=q_{l+1}$,且 $\{p_{l+1\cdots l'}\}=\{q_{l+2\cdots l'+1}\}$,这又表明 $q_{l+1\cdots l'+1}$ 必须是上升段且除了 $q_{l+1}$ 外其余都大于 $q_l$。这一连串的推理表明除非在 $p_{1\cdots l}$ 就把 $k$ 用得只剩 $1$ 或 $p=\iota$,否则答案应当是 $f$ 中某一段卷上阶乘之和,这里 $f_i$ 表示 $l$ 排列中按照贪心分段恰好分 $i$ 段的数量,为 A003319 的 GF 的 $i$ 次方的 $x^l$ 次项。
CF1762F:考虑 $a_la_r$。这时可以维护目前贪心可以到达每个值的 $l$ 数,问题转化为区间求和,区间清空,单点改。
PA2021R1T1(lgP8386):判定型 dp 是 $f_i$ 表示前 $i$ 个能否消光,$f_i=\bigvee_{j
AGC064D:考虑如何判定。可以将最终从底向上写的序列理解成一棵树的 dfs 序对应的字符,这棵树编号满足大根堆性质,且儿子从小到大排序,且非叶子对应的字符均为 B。考虑从大到小生成这棵树,每次加一个叶子。现在回到序列角度,相当于初始有个 B,倒扫,每次将当前字符插到某个 B 后面。可以将一个 B 及其后面连续 R 看作一个整体,用单个变量表示后面有几个 R,那么对原序列的插入可以理解成对变量序列 $x$ 的操作:插入 R 就是某个 $x_i\xleftarrow{+}1$,插入 B 就是在非末尾插入一个 $0$。设 B 有 $b$ 个,那么合法条件就是若干不等式:$x_b\ge$ 某个值,$x_b+{}$前 $b-1$ 个中最大值 $\ge$ 某个值,$x_b+{}$前 $b-1$ 个中最大值 $+$ 次大值 $\ge$ 某个值,等等。那这就和 CF1740F 很像了(只不过这题有序)。$f_{i,j,k}$ 表示前 $i$ 大,和 $j$,目前考虑值为 $k$。$x_b$ 单独决策,作为初值。转移得枚举为 $k$ 的数量,复杂度 $\sum_i\sum_j\sum_{k\le j/i}(n-j)/k=\sum_j\sum_k(n-j)/k\sum_{i\le j/k}=\sum_j(n-j)j\sum_k 1/k^2=\mathrm{O}(n^3)$。
这题难点在从后往前考虑。我所考虑的 dfs 树其实就是帮我想到倒过来考虑的一个跳板而已。
[CTT2023] 黄焖鸡:判定方法是,扫描右端点,维护每个左端点的 $(f_0,f_1)$ 表示当前位不选/选,选减不选的最大值,新加一个数 $a$,$(f_0,f_1)\circ a=(\max(f_0,f_1)-a,f_0+a)$。如果 $\max(f_0,f_1)=0$ 就爆了。组合性质或归纳易证以下性质:$f_0+f_1\ge 0,\lvert f_0-f_1\rvert\le 2m$。考虑什么样的对没前途,即永远不会导致不合法。$f_0>0$ 肯定不用管;假设后面又接了一段序列,奇数项和为 $s$,偶数项和为 $t$,$\max(f_0+s-t,f_1+t-s)=0$ 必须有可能出现(不可能 $<0$),综合 $f_0+f_1\ge 0$,得到 $f_0+f_1=0$,这时只需后面加一个 $f_1$ 就爆了。因此只有 $(-1,1),\cdots,(-m,m)$ 有必要记,可以状压。转移形如:要求第 $i$ 位为 $0$,将低 $i-1$ 位 reverse,第 $i$ 位置 $1$,其余置 $0$,容易感知到一个 $2^m+2^{m-1}+\cdots$ 的去掉一个 $m$ 的突破口,用一个类高维前缀和优化填表法即可 $\mathrm{O}(n2^m)$。
其他. [NOI2022] 移除石子、[ZJOI2019] 麻将
第三步 设计 dp
这里首先要排除掉非生成类 dp 也就是一般的递推式的设计方法。这类问题难点单一,关键在于找到一个封闭(可以转移)的状态描述,然后填表即可。技巧性不强,因此后文不讲。
例:
CF1778D:$f_i$ 表示有 $i$ 个 $1$ 的答案,$f_i=\frac{i}{n}f_{i-1}+\frac{n-i}{n}f_{i+1}+1$,有点难解。整理得 $i(f_i-f_{i-1})=(n-i)(f_{i+1}-f_i)+n$,换元 $g_i=f_i-f_{i-1},g_n=1$,然后递推即可。
CF1667E:(解 1)$u$ 为重心,一方面 $u$ 子树以外的点 $n/2$ 的方案数 $f_u$ 容易算,然后答案 $g_u=f_u-\sum_{v>u}g_v/u$。这个 ${}\div u$ 可以从概率的角度理解——$v$ 是否为重心与前 $u$ 个点树形无关,且可以将前 $u$ 个点视作不可区分的,故 $P(v\text{为重心}\mid v\text{在}u\text{子树中})=1/u$。
(解 2)一个不递推的推式子做法。考虑删去 $u$ 后有个连通块 $siz>n/2$ 的方案数,补集转化,分类 $u$ 子树和 $u$ 以外两种情况讨论,枚举 $siz$。最终会得到一个卷积形式。
其他. CF1534F2、+CF1770E、dmy stars
对于生成结构类 dp,设计 dp 是解题的核心。在考虑具体的设计前,先思考一个问题:dp 到底计算的是什么?
对于一个有待定信息的结构,每个 dp 状态以及值都表示确定待定信息中的某一部分,所有满足某些条件的解(即确定内容)它们的一个概括量。这些条件就是状态,概括量就是 dp 值。
因此考虑 dp 的前提是,先明确这个结构以及其待定部分是什么样的。这里我想表达的是,建议在做完前两步后进行一个小结,明确 dp 的对象,以及其特征与性质。这样有助于后续思考清晰。不要认为这是废话,出现混淆状态含义等设计失误往往是因为没有明确 dp 对象造成的。
几个原则
好,接下来我先列出 dp 设计的几个原则,再详述思考方式。
众所周知,严谨地来说,一个 dp 的要素包括:最优子结构、重叠子问题和无后效性。但在实际设计时,一般会考虑这三点:
- 每个希望被考虑(合法,或可能成为最优)的解均被恰当地(主要指计数题中次数正确)计入,不希望被考虑(不合法但会影响答案)的解均不被计入。这决定了无论在设计 dp 还是验证 dp 时,我们都会想象一个解,然后考虑它被计入的情况。“考虑一个解被计入的情况”,这是非常重要的思考习惯,因为当这样考虑时,可以跳出当前 dp 生成过程的语境,不被组合意义限制,去考虑本质上要记的东西,找到一些非常规的 dp 方式。
- 状态数足够少。换句话说,可以将“确定待定信息中的某一部分”这个确定部分视作一个黑盒,其只有少量的信息会与剩余待定信息以及所求限制产生互动关系,一般体现为确定部分的某些数量特征或边缘(某个邻域)的确定情况,在题解中往往会以”我们只需记录某类信息/只需求某类子结构的答案“出现。
- 状态是封闭的。这个更好理解,其实就是重叠子问题的意思。如果状态不封闭,那么从某个状态出发就会推出或依赖更多的状态,进而导致状态数爆炸,子问题的重叠情况就不够密集。这个可以类比分治类数据结构的信息封闭性来理解(例如推复杂线段树的记录信息与 tag)。同时这个要求会引出一类 dp 的设计方式,详见从转移推状态。
在设计 dp 前,应当有以下几个意识:
- 优先考虑优化暴力 dp 和推广特殊情况 dp。相比凭空定 dp 状态,这两种方法显然更容易。不要急于一次性将高度优化或有复杂细节处理的最终 dp 想出来。
- 优先考虑组合意义,优化时结合组合意义。用数学方法或形式化描述容易把自己搞晕,或丢失性质。
- 优先寻找突破口,而不是一味地强制钦定某个顺序或规定状态定义再硬推转移。突破口可能是某个贪心性质、结构简单特征、信息量小或限制多的子结构、无关性或独立性等等。
设计方法
注意,这里会讲得比较抽象和概括。dp 设计有非常多零碎的技巧,尤其是关于局部生成时序和状态选择相关,这些会在例子中提及。建议看理论的同时结合例子。
好,现在是主要的两类 dp 设计方法。
第一类是设计生成过程,再确定状态。首先确定一个解大致的生成顺序,然后确定生成过程中的部分结构或时刻,用状态去表出这部分,用转移表出状态之间的部分。值得注意的是,状态相同时可能有不同的转移方程。
该方法的核心以及难点就在于生成顺序的选取和子结构的选取。首先所谓的“生成顺序”绝不仅仅代表线性地扫一遍的顺序,因为难题的模型可能有多个维度(例如元素是区间,结构是带时间维的过程,带别的权值等等),有复杂的限制条件,或者结构本身就不是线性的。其次对于大致相同的顺序,子结构的选取就像在生成过程中寻找一些“checkpoint”,选取的不同会导致需要记录的信息量的差异。
有些特定的结构有常用的生成方法,但诚然不存在通用的定法,有时只能靠枚举试错。但还是有些好的思考习惯。首先既然说是“想象法”,那就必须对静态和(以各种顺序)动态的模型有清晰的认知,在纸上画图,明晰模型在生成过程中呈现的特征,从而发现信息量小的部分(即突破口)。从否定的角度来说,可以尝试先排除不可能的方向,剩余少量可能。另外在设计状态时要尝试寻找不必要的状态(不可能、去除该状态也能对)以及不必要记的信息(可以合并、可以不管、可以多并一)等等。
第二类是关注单步决策,推理出状态。这种方法可以先确定大致的顺序或先后关系,也可以不确定。关键思想在于,先通过观察(顺序未知的)生成过程中某个静态的片刻或局部(只考虑某一步),发现无关性,作为定状态的突破口。思考过程一般是,首先寻找结构的单个决策(往往是最终结构,即考虑最后一步),然后分析该部分与剩余待决策部分的关系(可以想象该部分已确定或去除该部分之类的),得到剩余部分必要的限制条件或信息。如果出现多个无关部分就拆开来。反复进行上述操作,不断扩充状态使其关于转移封闭即可。这个有点像某些 ds 设计复杂 tag 的过程。
这个思路更符合 dp 原本的定义,但是如果模型中与单步决策相关的信息太多,会导致状态不确定性太大,由于这个思路靠的是找必要性,故容易定不出状态,这时就得用第一类方法——先确定生成过程,本质上就是通过猜一部分状态相关的信息来减少不确定性。但是如果第一类方法猜不出来,例如下文中某些奇怪的树型 dp 和断点转移,以及上文的 CF1781F 和 CF1439D,就可以用这个方法,较容易地获得状态设计线索。但相对来说这种方法用得并不多,要不就出现在较难的题里。
无论如何,这两类方法并不是泾渭分明的。例如第一类方法定出的状态数太大,再结合模型特点与转移微调状态;第二类方法也可以猜一部分的生成顺序。
另外提及一下两类对立的 dp 特征:单步转移和断点转移。这个分类源于与 crn 的讨论(原话的第一种是“逐步转移”)。单步转移的 dp 每次只决策一个“最小单元”,而断点转移更像“跳跃”,一次性决策连续的待定部分(利用数学方法或其他性质)。在数据范围允许的情况下,一般建议单步转移,因为更易写转移方程,且不容易漏性质;断点转移往往在单步转移状态量太大(指数或多了若干维)时用于缩状态,但往往转移需要优化。一个经典的例子是在一个序列中选多个位置时,单步转移需要记两维,而断点转移可以规定当前末尾必选,然后用一些优化解决。
注意单步和断点的对立是相对而言的,有时单步转移的也可能是较长的一个部分。可以结合例子理解。
这里,再强调一下一个重要的性质——无关性,或者叫独立性,这是 dp 的重要信号。这种性质分为两个方面,一是当前步决策与先前步决策情况无关或关系较小(只需记少量变量),这在最优化 dp 中体现为最优子结构(只需规定少量限制,就可以保证候选解包含全局最优);二是多个不交部分间的决策无关(也就是第二类方法利用的),而它们在某处汇聚。这两个特征共同导向的重叠子问题,也就导向了封闭且足够少的状态。
转移方式
关于看待模型的方式对转移方程的影响,这里有两类情况。
第一类是填表法,指对于当前状态找出它可能的前驱状态来求得自己的答案;第二类是刷表法,指对于当前状态找出它可能的后继状态去更新它们的答案。
这两个名词我也不知道是从哪里来的,据说很多初学者就知道。这里主要想讲一下这两类转移的思路差别。
在构造题方法总汇中,我提到一类构造方法是 k. 归约法和增量法。这两种方法的大思想相同,但具体思考方式有差别。dp 也是一样,考虑一个结构删去(可能先待定)或确定某个部分后,剩余部分如何归约,这就是填表法;考虑一个未完成结构上增加一些部分后信息的变化,这就是刷表法。
在一些结构较简单的题中,这两种方法是相通的,一方面转移简单时可以直接转换,另一方面可以将 dp 确定部分和未确定取反(可以理解成“起点到它的方案数”与“它到终点的方案数”这两种),通过改变状态定义中的方向来转换。但情况复杂的时候只有一种是可行(或容易思考)的,所以要多换几种思考方式。
例
CF354D:将金字塔顺时针转 $45^\circ$,视作直角三角形。方案形如:
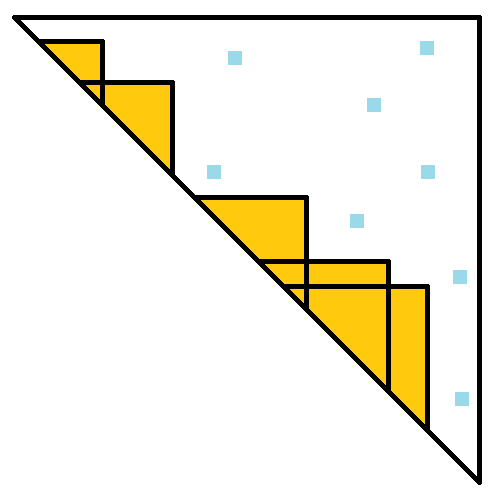
且每个小三角边长至多 $\sqrt{6k}$ 左右。(解 1)最直接的思路是对小三角 dp,断点转移。可以记当前的最右竖边(这条边对应的直线前面的全部考虑完),转移时枚举(上一个小三角竖边)和(当前边长)之一,另一方的选择可以优化掉。注意上一个不交时应当先单步(不选)转移到当前开头,强制相交。
(解 2)类似扫描线,逐行或逐列扫描,记录当前最右或最上的被小三角覆盖的坐标。新开小三角形可以断点转移也可以单步转移,取决于怎样计入小三角的代价。
这题的灵活性很强。其实大致的生成顺序都是一样的,就是局部的先后关系和计代价的拆分方式有些差异。解 1 的优点在于整体思考每个小三角形,状态较简洁,易推广;解 2 的优点在于转移容易想。这题是从状态推转移。
(落月摇情满江树)(给定一棵儿子有序的有根树,所有相邻叶子额外连边,求能否将点划分成若干简单环):(解 1)考虑一个子树的情况,如果有非完整环那么要记下,与外部产生关系。发现仅有四种:全完整、最左叶子到根路径、根到最右叶子路径、最左叶子到最右叶子路径。从所有儿子转移,做到线性需要一些处理。
(解 2)考虑逐个儿子加入,方便讨论转移。此时状态除了原来的四类外还有(根未覆盖,其余完整)和(根未覆盖,最左叶子到最右叶子路径)这两种。对于六类情况分别讨论在最后一个子树和前面部分如何拼合可以得到即可。解 1 和解 2 的关系有点类似断点转移和单步转移的关系。
这题非常形象地体现了“状态封闭性”要求。要求确定状态集合使得转移能够自洽,这就像每个状态都是一个拼图,要能完美地吻合起来一样。
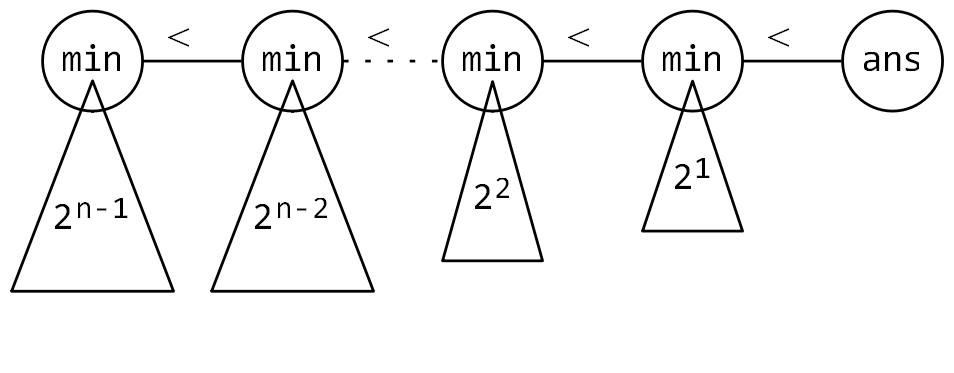
CF1784D:结构如图(ans 表示获得 Wooden Spoon 的人):
乍一看不容易 dp,先考虑静态模型。和上文中排列的部分题很像,都是有一些主要元素,其余元素与其中一个有偏序关系这么一个拓扑序计数。这一题中对主要元素有绝对大小的要求,故只能从右往左钦定。对于深度为 $i$ 的点(根深度为 $1$)其下面挂的子树 $\min$ 为 $j$,那么它贡献倍数为 $\binom{2^n-j-2^{n-i}}{2^{n-i}-1}$。而这只与 $i,j$ 有关。
第一种思路是枚举获得 WS 的人,然后从右往左 dp,但这样至少带 $2^{2n}$。(解 1)从左往右 dp 时,由于目标限制出现在状态中(获得 WS 的是某个人),故可以。$\mathrm{O}(n2^n)$。
(解 2)第三种思路是按值域从小到大填入。记录当前前缀中几个子树至少填了一个数,单步转移即可。
CF1765C:问题转化为对于 $l=1\sim k$,求任选 $l$ 张牌,最少的有 $c_0$ 张的概率。如果已知四种分别有 $c_{1\cdots 4}$ 张,那么概率为 $\binom{n}{c_1}\binom{n}{c_2}\binom{n}{c_3}\binom{n}{c_4}/\binom{4n}{l}$,(解 1)因此可以枚举 $c_0$ 后卷积,得 $\mathrm{O}(n^3)$。(解 2)$\mathrm{O}(n^2)$ 的做法是,按数量从大到小 dp。令 $f_{i,j,k}$ 表示当前上界是 $i$(接下来钦定的牌至多单种 $i$ 张),已定牌数为 $j$,已定了 $k$ 种牌,每次确定当前这个 $i$ 钦定给几种牌。(解 3)这题可以从小到大,只需将猜测成功率作为 dp 初值即可,相当于多个 dp 合并起来做,这是官解。
这里有两个技巧,一是背包的单步转移,实际上解 2 和解 3 的 dp 数组同时承担着两种定义(这个在背包专题例 4 中也提到):当前最少的是 $i$ 张,和当前最少的 $\ge i$($\le i$)张。根据是否允许转移给不变的 $k$,可以区分这两种定义(解 2 更新答案时 $k$ 必须变)。二是解 2 和例 3 相同的技巧:通过改变 dp 顺序,使得目标限制和(终)状态吻合,减少一维枚举或状态。这是想象顺序生成的重要技巧。
CF1060F:先枚举最后得到的节点 $r$,然后完全不会定状态。这时考虑以 $r$ 为根,所有儿子的子树是互相独立的,这就得到了 dp 的启发。每个儿子的子树要求的都是内部先合并若干次,然后 $r$ 在某一时刻合并上它了,之后再合并若干次,得到的仍为 $r$ 的概率。因此考虑 $f_{u,i}$ 表示点 $u$,内部剩余 $i$ 次合并时,$r$ 从上面下来和 $u$ 合并了,最终仍为 $r$ 的概率(这个概率只考虑合并时的 $1/2$,不考虑合并顺序,因为方便(考虑也行)。最后除以 $(n-1)!$ 即可)。分析转移发现这个状态是封闭的。具体来说,先考虑一个儿子 $v$,从 $f_{v,j}$ 转移。如果 $r$ 合并到 $u$ 在 $u$ 合并到 $v$ 之后,那么只从 $j=i$ 转移,因为从 $r$ 合并到 $u$ 开始计概率;否则,从 $j
你可能会有疑问:为什么要这样定状态?因为考虑一个子树内的边合并序列,根合并下来相当于在这个序列中某处插入一个分界。因此子树外面与内部产生关系的只与一个数量有关。为什么不令 $i$ 表示内部剩余含根的 $i$ 次合并呢?因为无法转移。另外,我当时在思考时又记了一维 $k$ 表示根恰好在子树中合并了几次(即,和“为什么”之后的这个含根合并的意思相同),然后最后让 $ans=\sum_kf_{r,n-1,k}/2^k$,这个得 $\mathrm{O}(n^5)$。正解对其的优化本质上就是将多个状态的值压成了一个,这也是很常见的技巧。
这题是典型的第二类方法。状态非常地怪,要真正理解可以从边合并序列的角度看,这启发我们要从多个角度同时看模型。同时还涉及了关于概率的处理,对于何时记概率,何时记方案数最后再除以总方案数的问题,答案是考虑转移时怎么方便怎么来。
CF771E:(解 1)正解的核心思想是,dp 只要使得任何合法解都能被生成即可,从而不必要记所有可能的状态。想象一个解,容易考虑一个类似归并的生成过程:当前如果接下来两行都是单行矩形,那么选右端点小的那个。也相当于不允许出现第一行右端点为 $i$,第二行右端点为 $j$,且 $nxt_ji$,故该状态所有的导出状态都不优于取到最大值的状态的导出状态。因此只需 1D,记对称的两个情况,刷表法转移即可。一个类似利用这个思想的是这篇题解,但是我无法理解他是怎么想出这个“不必要”条件的。另外还有一种见鬼的记搜解法,如果您知道它的状态数证明请告诉我。
CF1608F:只能从左往右生成。问题出在 $\operatorname{mex}$ 被更新时的连锁增加,这就会要求记录已决策的数中 $>\operatorname{mex}$ 的 bitmask,那就完了。但是仔细一想:真有必要全部决策吗?是不是在连锁增加时有用才决策更好呢?因此考虑 $f_{i,j,k}$ 表示在 $i$,$\operatorname{mex}=j$,前面 $>j$ 的有 $k$ 个的方案数。当 $\operatorname{mex}$ 更新时,枚举连锁更新的量,用组合数分配即可。然而由于得枚举 $k'$,故无法避免 $\Omega(n^3k)$。
考虑将 $k$ 的定义改成“有 $k$ 种”,这样转移时只需要让 $j$ 单步即可。转移系数的下降幂妨碍单步,可以拆开来分给转移的起点和终点,也可以在定等价类时先决策大小关系。$\mathrm{O}(n^2k)$。
这题的延后决策技巧是局部生成时序的典型例子。从另一个角度理解,相当于 dp 已决策部分为下标—值域平面上的一个左下角矩形。这个矩形的上方既不能先决策,也不能完全不决策。
[联合省选 2021] 滚榜:初步思路是逐个确定,记当前的状压、末尾编号,末尾 $b$ 与 $\sum b$。优化,考虑记 $b$ 的目的是保证 $b$ 递增以及 $a+b$ 递增。而相邻的 $b_x\le b_y\Leftrightarrow b_y-b_x\ge 0$,$a_x+b_x\le a_y+b_y\Leftrightarrow a_x-a_y\le b_y-b_x$,可以考虑差分数组,$\Delta b$ 的下界是 $\max(a_x-a_y,0)$,同时这些下界可以确定一个 $\sum b$,只需要它 $\le m$ 即可。那就不必记末尾 $b$ 了,$\mathrm{O}(2^nn^2m)$。
这题实质上决策的东西没有变,只不过换了一种方式刻画已决策部分的影响。可以通过画出 $b$ 的柱状图然后换一个方向看来得到突破口——原来记的和是左下角的三角形,现在记的是下方的一个梯形。这题也可以算是状态合并的例子。
[IOI2020] 装饼干:也是个判定型计数,考虑题目条件更好的描述。首先有个简化,如果 $a_i\ge x+2$,那么它可以合并一对。然后,合法的充要条件是,$y$ 的低 $i$ 位的 $x$ 倍必须 $\le \sum_{j=0}^{i-1}a_j2^j$,充分性的构造是,从高位到低位贪心使用下标大的,或从低到高随便用。如果从低到高,那就得记一个当前剩余可用和,不好优化;如果从高到低,考虑钦定了一个最高 $1$ 位 $i$,它往下贪心用掉,最后一个用掉的是下标为 $j$ 的,且其剩余 $a'_j$。
如果 $a'_j=x$(不可能再大了),那么次高 $1$ 位至多是 $j+1$,并且如果次高 $1$ 位 $\le j$,那最高 $1$ 位实质上不产生影响,因此是一个无关的子问题;如果 $a_j'
这题是一个从转移推状态的例子。由于发现决策时只有一种情况会被影响,其他情况都可以归为形式相同的子问题,那就找到了 dp 突破口。
[ZJOI2022] 树:初步思路是逐一钦定每个点在哪棵树中是叶子,第一棵树要记录当前非叶子数与已有至少一个儿子(已满足)的非叶子数,第二棵树由于是倒过来,故生成模型变成了一个若干子树合并到当前点的形式,记录当前子树数,若是非叶子则枚举选几个作为儿子。这样一共是 4D/1D 的。分开来看每棵树,考虑以下思路转变:
第二棵树记子树数必然导致一维卷积,得改。实际上其状态可以和第一棵树类似——记录当前尚待决策的点中有几个是非叶子以及满足的情况。这实质上是先前提到过的“将 dp 确定部分和未确定取反”的技巧,相当于第一棵树是不断生成,第二棵树是不断消去。
为保证非叶子所记的另一维需要消去,可以用容斥——不保证非叶子有至少一个儿子,而钦定非叶子时新增一个强制它无儿子的 $\times (-1)$ 的转移。
保证非叶子可以用另一种方法:在一个非叶子的最后一个儿子处将该非叶子的“接口”删掉,即,将非叶子数减一(第二棵树就是在第一个儿子处加一)。这个和 USAC23JANPlatinumT2 中只在钦定的最后一次访问某个点时才修改 bitmask 对应位置的思路异曲同工。
这样就 3D/0D 了。第一个优化本质上是决策时序的微调,将决策叶子同时决策儿子改成决策叶子同时决策父亲。第二、三个优化单纯就是改变当前刻画信息的方式。这题深刻地说明了几个事情:确定了大的生成顺序并不意味着局部决策顺序唯一,确定了精确的决策顺序并不意味着状态唯一,确定了状态并不意味着方程唯一。
[联合省选 2022] 最大权独立集问题:只考虑有两个儿子的情况,称先交换的儿子为左儿子。根的左儿子子问题为 ① “父亲点权为初始点权,$u$ 子树(含父亲边)完成交换,最后传给父亲的权为 $d_x$ 的最优解”,右儿子子问题为 ② “父亲点权为 $d_x$,$u$ 子树(含父亲边)完成交换的最优解”。继续往下看子问题 ②:
父左右。子问题为 ③ “$u$ 点权为 $d_x$,$u$ 子树内(不含父亲边)完成交换的最优解”。
左父右。左儿子换给 $u$ 的点权会额外贡献一倍,需要记;换给右儿子的点权为 $d_x$。因此左儿子是一个子问题 ①,右儿子是个子问题 ②。
左右父。$d_x$ 恰好贡献一倍,$u$ 在与父亲交换前的权值也额外贡献一倍。子问题为 ④ “$u$ 点权为初始点权,$u$ 子树(不含父亲边)完成交换,最后 $u$ 的权为 $d_x$ 的最优解”。
子问题 ① 是对称的。然后看子问题 ③。这时必须枚举左儿子交换上来的点权,导致三次方。但是,这里的一个直觉是,这个左儿子交换上来的点权和 $u$ 当前的点权 $d_x$ 很大程度上是无关的,也就是不必嵌套而是可以分开枚举。这个直觉可以通过分析左儿子的交换情况得到(令 $u$ 的左右儿子分别为 $v,w$,下面的父、左、右指 $v$ 的父、左、右):
- 父左右。$v$ 还是子问题 ③,$w$ 是 $x=v$ 的子问题 ①。
- 左父右。$v$ 左儿子传上来的点权会交换给 $w$,$u$ 传下去的点权会给 $v$ 右儿子,因此这两个权值它们不会共同影响一个子问题,或者说它们的贡献是用加法连接,可以拆开的。因此,先把 $v$ 左儿子的这条路线的最优解算出来就行了。$v$ 左儿子是子问题 ②,$w$ 是子问题 ①,$v$ 右儿子是子问题 ①。
- 左右父。这时 $d_x$ 恰好贡献一倍,与 $v$ 交换上来什么无关。因此可以不枚举 $x$ 但枚举 $v$ 交换上来的点权就算出答案,$v$ 为子问题 ④,$w$ 为子问题 ①。
如果从公式角度看,这个三次变两次的过程实际上就是通过再往下讨论一层,使转移 $f_{u,x}=\min_yF_u(x,y)$ 变成了 $f_{u,x}=\min_y\{G_u(x)+H_u(y)\}=G_u(x)+\min_y H_u(y)$。所以说在解题过程中要对独立性非常敏感。另外这题也是状态推转移的很好的例子。
THUSC2023D1T2:尽量避免记燃料和能量,能量很傻,直接分段。现考虑不补充能量的一段的最优解,关键思路是将状态定在补给燃料的位置,这样只需记当前的区间与所在点。断点转移会五次方,考虑到转移范围是一个一维偏序,故只需用 ds 维护当前右端点的所有可能转移,到下一个游乐园理解成全体位移 $w$ 即可。同一个右端点内部预处理两两最短路即可。$\mathrm{O}(n^2m^2+n^2m\log{})$。
这题的难点是选取合适的子结构。
[NOI2023] 桂花树:默认已知 $T'$ 的结构刻画。对相对值域 dp 不可行。
(解 1)条件 2 可以描述成“点 $u$ 的儿子中至多有一个,其子树 $\min
(解 2)考虑从小到大加入点,即考虑编号前缀点在 $T'$ 中的虚树。可以在随意的位置加一个叶子,裂一条边,或有条件地加一个 $\operatorname{lca}$ 尚未加入的叶子,这个 $\operatorname{lca}$ 会有一个编号大小的限制,要记一个状压。也可以理解成一个部分延后决策。$\mathrm{O}(mk2^k)$。
这两个做法,一个是从大到小填表,一个是从小到大刷表,而最终的解法本质上恰好是差不多的,是同一种生成思路的断点转移和单步转移形式。
[NOI2023] 深搜:还是判定型计数,两个思路:直接对边集计数(记录是否存在至少一个关键点满足),枚举点集容斥。都先考虑特殊性质。
(解 1)直接对边集计数,性质 B:$f_{u,d,0/1}$ 表示一端在点 $u$ 子树内的非树边已定,选的非树边最浅达到多少的深度(与 $dep_u$ 取 $\min$),子树内是否有满足的关键点,这样的方案数。这个可以整体 dp:如果有多于一个儿子内有跨 $u$ 的非树边,那所有子树中的关键点都废了;如果恰有一个,那当前 $0/1$ 取决于该儿子的 $0/1$;否则直接乘起来。这些都可以线段树合并。正解:横叉边会限制关键点只能选在一或两棵子树内,这一或两棵子树内是独立的,因此有希望结合原 dp 解决。先解决只有一棵子树可以的,枚举该子树根,从它出发至少有一条横叉边,两端都在它外部的非树边可以换根 dp 解决。现在只需容斥掉有两棵子树均可以的情况:
以 dfs 的方式枚举 $u$,用 dfs 序上的线段树维护所有可能的 $v$ 的系数:对于一个 $v$,$\operatorname{lca}$ 是定的,因此这两者之间的返祖边方案数易求(必须两端均在链上或均在链上点某个非链上儿子子树内),同时两端分别在 $\operatorname{lca}{}-u$、$\operatorname{lca}{}-v$ 上的横叉边也在 $v$ 处维护,是形如区间乘 $2$ 的更新,然后再是 $v$ 子树的答案,这三者的乘积。对于一个 $u$,枚举选以它为一端的横叉边 $e$,现在要求其他以它为一端的横叉边的另一端都是 $e$ 的另一端的祖先。然后就是一个区间查询,再乘上与 $u$ 相关的系数和 $\operatorname{lca}$ 向上的部分。注意由于要强制 $v$ 有至少一条横叉边,故要对 $u$ 出发新的横叉边的另一端和另一端子树内其他点分开讨论一下。
这个做法我只是口胡了一下,实际写起来会极度复杂。如果您发现这个做法有锅请指出。
(解 2)(来源)还是看原题解比较好。大致思路就是容斥,边只能完全在钦定的关键点的虚树单边内或单边内点的其他邻点的子树内。然后这个东西在性质 B 时就要断点转移(解 1 是单步),但可以 ds 维护;优势在于有横叉边时只需枚举顶部,“稍加”讨论即可。
([原创] 禁止套娃)(求一个序列所有本质不同子序列的本质不同子序列个数之和,$n\le 5000$):首先有个经典的算本质不同子序列数的线性 dp,也就是钦定单射,只对最左匹配计数,要求选的相邻两数之间不能有等于后者的。考虑仿照其思想:
设选择的外层子序列下标为集合 $I$,内层为集合 $J\subseteq I$。为了方便表述,设占位下标 $0\in I,J$。同样只计贪心匹配的情况,限制如下:
- $I$ 中相邻两个数 $i,i'$,$a_{i+1\sim i'-1}$ 中不存在 $=a_{i'}$ 的值。
- $J$ 中相邻两个数 $j,j'$,$a_{I\cap(j,j')}$ 中不存在 $=a_{j'}$ 的值。
考虑对 $J$ dp。$f_i$ 表示目前考虑到 $i$ 且内外层末尾均选 $i$ 的答案。如果要从 $f_j$ 转移过来,那么就要决定 $a_{j+1\sim i-1}$ 这部分如何选外层,设选择了集合 $K$,限制如下;
- $K$ 中相邻两个数 $k,k'$,$a_{k+1\sim k'-1}$ 中不存在 $=a_{k'}$ 的值。
- $K$ 中最大值 $k_r$,$a_{k_r+1\sim i-1}$ 中不存在 $=a_i$ 的值。
- $K$ 中任意 $k$,$a_k\ne a_i$。
一个简洁的处理方法是,对于每一个 $i$,dp 出 $>$ 每个 $j$ 的只需满足 1、3 条件的本质不同子序列个数 $g_{i,j}$,真正转移时 $f_i\xleftarrow{+}(g_{i,j}-g_{pre_i,j})\cdot f_j$ 即可。最后汇总答案可以弄一个必选的占位下标 $n+1$。
这题其实不难,关键是把结构看清楚。
[互测 2021] Imbalance:(参考)只讲 Subtask 3。描述计数限制:$s_i$ 表示前 $i$ 个中 $1$ 的个数,$s_i-s_{i-1}=0/1,s_i-s_{i-k}\ne k/2$。像题解中一样将 $s$ 排成矩阵,暴力状压实际上是先行后列的轮廓线 dp,而先列后行在 $k$ 大时状态数更少,这就像一些二维问题状压 dp 前 if(n<m)swap(n,m);。又由于只需考虑所有 $s_i-s_{i-k}$ 全部 $<$ 或 全部 $>k/2$ 故可做到题解中的复杂度。这题也是观察与生成顺序很大程度上影响状态数的有力说明。
[互测 2023] Tree Topological Order Counting:想象某个拓扑序,一个点 $u$ 的祖先都在 $u$ 前面,且他们各自的不包含 $u$ 的儿子子树在他们后面随意穿插。而这题又得固定 $u$ 的绝对位置,因此就和 CF1784D 相似,这题我用的单步转移思路。外部子树的后续占用情况不宜直接确定,因此考虑记 $f_{u,i}$ 表示 $u$ 在第 $i$ 位的方案数,这里的方案数包含外部子树内的拓扑序数量(形如 $n!/\prod siz_i$),以及他们在 $i$ 之前的部分的方案,但不含在 $i$ 后的(但数量已知且相对顺序已决策)。对于一个 $v$,先加入非 $v$ 儿子子树并穿插,再往后塞若干数,再塞 $v$。这题更能看出局部时序的技巧——往往要决策,但只决策一部分信息。
[互测 2023] 雷同:同样考虑合并树,同样书的深度随重量递减,同样想象最优的树的生成过程。这里我考虑的是自底向上合并:如果书的深度均确定,那么过程可以看作,从大到小扫深度 $d$,每次加入当前深度的,然后两两合并,点上记一下磨损度。易发现按磨损度排序后两两合并是最优的,调整法易证这是个“下界”。立即可以得到一个 $\mathrm{O}(n^3\log{})$ 的区间 dp。
考虑直接对叶子形成的折线 dp,如果从浅到深 dp,必须记深度和剩余允许的同层叶子数,多了个 $\log$。如果从深到浅,则不必记深度,只需记:以目前已生成叶子的 $\operatorname{lca}$ 为根的子树,将其视作 01 trie,到当前叶子的路径状态。转移包括直接定一个叶子和上移一层,其中后者可能导致根变,要加一个重量的前缀和。时间平方。
容易发现,后一种 dp 更优的根源在于,其计算代价的方式从逐叶子变成了逐层,这与 [联合省选 2021] 滚榜 的思想一致。
待填坑. [UR #20] 跳蚤电话、[UNR #7] 璀璨宝石
第四步 优化 dp
首先要明确一点:最好的优化 dp 的方法,是做好前三步,或在较劣的 dp 基础上重做前三步。很多时候 dp 不够优,要么是漏性质,要么是观察角度或结构生成方法不对。对着复杂的转移方程做一堆细节很多的优化,不如先重新审视模型,改变 dp 思路。当然有的题优化也是必需的。
优化 dp 的第一步是观察清楚现有的 dp。观察的角度包括:
- dp 的组合意义。清晰的组合意义不仅能使一般的优化变得容易,还能提供“dp 方程之外的东西”。例如表达状态更本质的方法、不必要的状态和转移、转化状态的可能性、dp 的决策单调性等等。
- dp 的转移方程。这里个人建议在草稿纸上写清关于 dp 的所有信息:状态定义、转移方程、转移顺序、初值、终值、时间复杂度。通过写清这些东西,可以找到一些通用优化方法适用的特征,或是直接对方程进行数学方法处理。同时对写代码也有帮助。
- dp 的转移图。主要包括基于原模型的 dp 转移示意图和基于 dp 转移的表格图。可以较直观地找到优化方向,处理一些细节。
dp 的优化分为对状态的优化和对转移的优化。注意,下面列举的许多优化都可以且建议在第三步设计 dp 的同时完成,而不是写出一个暴力 dp 后在其基础上优化。先讲对状态的优化。
状态数的自简化
有时,真正可能 dp 到的状态远少于 dp 状态每一维最大值之积。可能使用记搜简化代码。
例
其他. CF1188C、+CF662E、+CF771E、+CF1740F
下标换元
令 $g_i$ 表示 $f_{t(i)}$ 然后对 $g$ 做 dp,这样的一个换元优化不仅能方便一些转移优化,还常能暴露出一些不必记或不必分开记的状态,触发状态数的自简化或状态合并等,从而减少状态数。建议从组合意义角度入手优化(微调状态定义)。
例
- CF1801F:如果记 $f_{i,p}$ 表示当前 $b$ 之积为 $p$,那是过不了的。考虑到剩余的 $b$ 应当满足积 $\ge\lceil k/p\rceil$,因此可以只记 $f_{i,r}$ 表示当前 $\lceil k/p\rceil=r$。对于一个 $i$,状态就只有 $\mathrm{O}(\sqrt{k})$ 个,转移再套一个整除分块,共 $\mathrm{O}\left(\sum_{i\le\sqrt k}(\sqrt{i}+\sqrt{k/i})\right)=\mathrm{O}(k^{3/4})$。
- CF662E:如果有 $\ge 90$ 个负的则答案为 $1$,否则显然考虑枚举每题属于哪一档,会得到一个背包,总共是 $6^3\cdot{30}^3\cdot90$ 这样。如果状态改为“剩下几个不被 hack”而不是“hack 几个”,总状态数就变为 $(30/2+30/4+\cdots)^3$,那就是 ${30}^3\cdot90$。
状态合并
在初步设计 dp 时,可能会设计一些含义较好理解的,但实际上有些信息没有必要区分的 dp 状态,可以在进一步分析时合并。
例
其他. [CSP-S 2019] Emiya 家的饭、+CF1060F、+CF1810G(解 1)
最优性去状态
对于最优化 dp,可以利用一些性质去除不必要记的状态,一般是这个状态不可能生成最优解,或有多条路线可以生成最优解,去掉其中的部分。思考方法一般是想象一个解,然后调整它。计数问题一般不用这个套路,因为要么可以归到自简化一类,要么优化前的 dp 会计重。
例
- [NOIP2023] 天天爱打卡:注意到使连续打卡段的起点是奖励区间的起点,终点同理,一定不劣。因此只需要在这些断点上 dp 即可。奖励部分是一个经典的扫描后前缀加,用线段树维护即可。dp 按归并顺序。
- [IOI2022] 鲶鱼塘:关键性质是:可以调整使每列的堤一定建在一条鱼的下方,或者空或满。但这样还不够,因为一条鱼可能被两个堤同时覆盖,从而计重,另一个性质是,不可能 $h_{i-1}\ge h_i\le h_{i+1}$,或者说结构一定形如若干空列分隔的单峰。这时转移的代价只需在一侧计即可。归并顺序+前/后缀 $\max$ 转移。
最优性换维
对于最优化 dp,这就是常说的定义域值域互换。有一类交换一维状态和所记值的优化,即,将求“某种情况下最优的……值”转为求“要达到最优值为……,某维的值至少/多要达到多少”。对于判定性 dp,如果 dp 值关于某一维具有二分性,或具有“只需关注最左/右的 1”这类性质,也可以将这一维压到 dp 值里。
注意,要刻意证明最优子结构。或者说,只考虑与记的最优值有关的转移,必然能把全局最优解/合法性求出来。
例
[UCup2Stage4] J. Joining Cats:考虑最后一步,比如是从左往右,那必定只有第一只猫是合并过的。因此任何时刻被合并的一定是一段。于是得到一个 3D 的判定性 dp,有两个压的思路:对一个区间求最小并完时间,对一个左端点和一个时间求最大右端点。刷表,每次要求一个点向左/右最远可以合并到哪里,这个可以双指针替代二分。
CF822E:暴力 dp 为 $f_{i,j}$ 表示 $s,t$ 分别匹配到 $i,j$,最少分几段。断点转移是一次决策一段,单步转移得再记维 $0/1$,表示当前段匹配是否完结。换维,如果保留 $j$ 则由于原 dp 存在一个 $f_{i,j}\rightarrow f_{i+1,j}$ 的转移,故转移难以 0D,因此考虑 $g_{i,k}$ 表示 $s$ 匹配到 $i$,分了 $k$ 段,最多匹配到 $t$ 的哪里。这时我就考虑也写成单步转移,结果错了。反例是 $s=\texttt{aaab},t=\texttt{aab}$,由于 $g_{2,1,1}=2$,故后面会断掉。这就是一个不具有最优子结构的例子,这题不能单步(您可能会问,如果对于每个 $j\le g_{当前}$ 都做呢?问题是并非每个 $j$ 都合法)。但断点转移是有最优子结构的(易调整法证明),得支持求两个后缀的 LCP,套 SA 或哈希+二分即可。
经验是,如果 dp 值用于决定转移的条件或位置,那就要当心最优子结构。
CF1091H:转化略。打表发现 SG 值至多为 $l=54$,这里用一个神奇的优化:从小到大枚举 SG 值,求出哪些情况的 SG 值为它。用刷表法,每当确定了一个位置,它的所有可能的前一步情况的 SG 值就不可能是当前值。这可以 bitset 优化为 $\mathrm{O}(lm+m^2\log\log m/(w\log m))$。这个优化相当于逆着用判定性转最优化,常用于最优化 dp 值域 $l$ 较小的情况,可以将复杂度除掉 $w$(如果转移比较好处理)或乘以 $l/w$。
CF936D:位置必须要记,这样的话状态里就不能记别的东西了。注意到如果摧毁一个障碍,那么必须经过它,且经过前不换行。但也不能记摧毁了几个障碍和装弹时间。这里就考虑 dp 值记录当前最长预留装弹时间,可以 $>t$,每经过一个障碍减 $t$,换行时与 $t$ 取 $\min$。最后改成断点转移来减少状态:换行只会出现在一个障碍物后面一格,因为晚换行不如早换行。这里建议先分析清暴力 dp 的方程,再改成离散化过的状态,更易写方程。以归并的顺序 dp 即可。
其他. [NOI2022] 移除石子、dmy guess
最优性去维
对于最优化 dp,有时性质较强,可以将状态维度移入最优化目标,形成一个 pair 形 dp 值且不损失最优子结构性质。一般来说性质形如“如果值不够优,那么另一维再怎么样也没用;如果值最优了,那就尽量使另一维更优”。这个性质一般通过分析数量关系或通过找样例守恒规律得到。
当最优性去维的性质强到一定程度,决策就变得单一,dp 就变成了贪心,如下面的例子。
例
CF1453E:走的是个 dfs 序,直接树形 dp 会涉及子树内答案和最后一个访问的叶子深度,不能做,因此可以二分后只记最优的最后一步深度。但这题有更强的性质:考虑一个非根点的所有儿子子树的最后一步深度 $h_i$ 都已确定,那么除了这个点最后一个走的儿子以外,其余的儿子的 $h$ 都要加一后取 $\max$ 给答案,而最后一个儿子的 $h$ 要加至少一,因为它要到子树外面去。故会选 $\min h$ 作为最后一个,归纳地,每个点子树最后一个必走最浅叶子。根特殊讨论。从而“最后一步深度”这维可以去掉,或者说变成一个待统计的定值。
[CSP-S 2019] 划分:(参考)有一个显然的 2D 暴力,打表发现最后一段尽量短是最优的,因此不用记第二维。证明考虑归纳+调整。设最后一段最短,前面也最优的解为 $P$,另一个解为 $Q$,它一定形如这样:
P: x|x|x x|x x|x x x|x x|x x x|x x x
Q: x|x|x|x x|x x x|x x|x x x|x x x x
即 $O$ 的倒数第 $i$ 个切点都在 $P$ 的对应切点前面(如果不是则可以调整证 $P$ 不优)。现在尝试调整证 $Q$ 不优于 $P$,发现直接硬调整是困难的。考虑直接从数值上证,即不增序列 $p_{1\cdots k},q_{1\cdots k}$,$p_1q_{j_2}$,这时将 $q_{j_1}\xleftarrow{-}1$,$q_{j_2}\xleftarrow{+}1$ 会更优。剩下就是每个位置求出以它结尾的最后一个切点 $f_{i}$,$f_i=\max\{j\mid s_i-s_j\ge s_j-s_{f_j}\}$,单调队列即可。
这个调整法很有教育意义。
[NOIP2018 提高组] 赛道修建:二分。剩下的 dp 需考虑内部已有的路径数和当前传上来未完结的直链长度。一个符合直觉的结论是,一定优先让内部路径数最优,再使当前直链尽量长。因为当前直链至多贡献 $1$,如果内部路径数不是最优,直链再怎么长也不会优,这和 CF771E(解 1)类似。于是问题转化为,有一堆数,要尽可能两两匹配使和 $\ge mid$,再最大化未匹配的最大值。一个性质是,如果最小值可以匹配,那一定有最优解中它匹配了,这个可以调整证。显然找 lower_bound 配即可,于是就归约下去。
其他. +CF771E(解 1)、CF1795F
扩大可行域
对于最优化 dp,可能为了保证解的合法,需要记录额外的维度;但有些不合法解它不可能成为最优,这时就可以默许它被考虑,从而减少要记的信息量。一个利用该思想的非 dp 问题是,定义一个序列合法条件,求一个序列的最长合法区间。区间会要求有一个一维偏序,但显然不考虑 $l\le r$ 也是可以的。
例
USAC23JANPlatinumT2:每个点的收益取决于最后一次到的时刻,但 $q$ 较大,故不能与询问时间相关,因此只能考虑每个点的亏损,但如果有点从未到达那还是会出问题,因此考虑枚举到过的点集(dp 刚好也要用上这些中间状态),这时对于询问相当于查某个 $x$ 的最高直线,可以处理出凸壳再回答。第二步完成,现在的 dp 对象相当于是给每个固定终点的点集安排一条线路,直接 dp 需要记录当前已耗时,不行;这时可以模仿 [联合省选 2021] 滚榜 的思路,直接考虑走一条边对之前的最后一次到达的点的亏损增量。$f_{S,i}$ 表示当前在 $i$,先前已经强制钦定最后一次到达的点集为 $S$($i\in S$)的最小亏损,枚举下一个点即可。
这里有两个问题:① 既然每次决策一条路径,那么如果又经过了已钦定“最后一次到达”的点那怎么计算?② 如果一个方案总时间大于询问的 $s$ 那怎么办?回答是:如果一个解违反了这两个问题中的合法条件,那么它一定不会是最优解,但最优解总是会被 dp 到的,所以没事。如果偏要考虑这两个问题,那 dp 就不容易了。
你可能会问:是怎么想到如此扩大可行域的?答案是优先考虑生成过程的完备性(涵盖所有合法解),暂且忽略纯粹性(不含不合法解),然后到头来再简单证明一下。也就是说这个设计过程是有些冒险的,但对本题模型的直觉告诉我应该没什么问题。他有一个“偏序关系”在里面。
[互测 2022] 翻修道路:对最短路树 dp。$f_{i,j,s}$ 表示目前根为 $i$,子树内关键点集合为 $s$,至多改 $j$ 条边权。当 $j$ 和 $s$ 不变时,所有的 $i$ 之间跑最短路互相更新;两个子树合并时,注意到 $f_{i,*,s}$ 递减,故决策一定形如归并,可以做到 $\mathrm{O}(2^knm\log m+3^knm)$。
这题的问题在于,dp 不能保证最短路树是真的最短,甚至不能保证是树,不能保证不会重复改同一条边的权!但是这些都是无所谓的,因为它们不会导致不合法的更优解。这题是一个经典的类型:要求 $\min_S\{f(S)\}$,然后 $f(S)$ 也是个 $\min$ 的形式,就直接用 dp 同时最优化这两个 $\min$。另外这题的生成思路和最小斯坦纳树相同。
(就硬推销自己的博客)您看这个问题的求解中第二步也用了这个技巧!
接下来是转移优化。
前后缀
对于一类转移范围为一个前后缀(或能转化为前后缀,例如利用可减性,或记次优值等等)且方程中的项都只与转移和被转移的其中一方有关的 dp,可以(换元后)用前后缀或类似预处理方法优化。通常用填表法会比刷表法方便,有时也可以用刷表,就是会变成差分。
前后缀处理优化实在是太入门了,这里就不给例子了。
例
其他. USACO21OPENPlatinumT3
多步拆单步
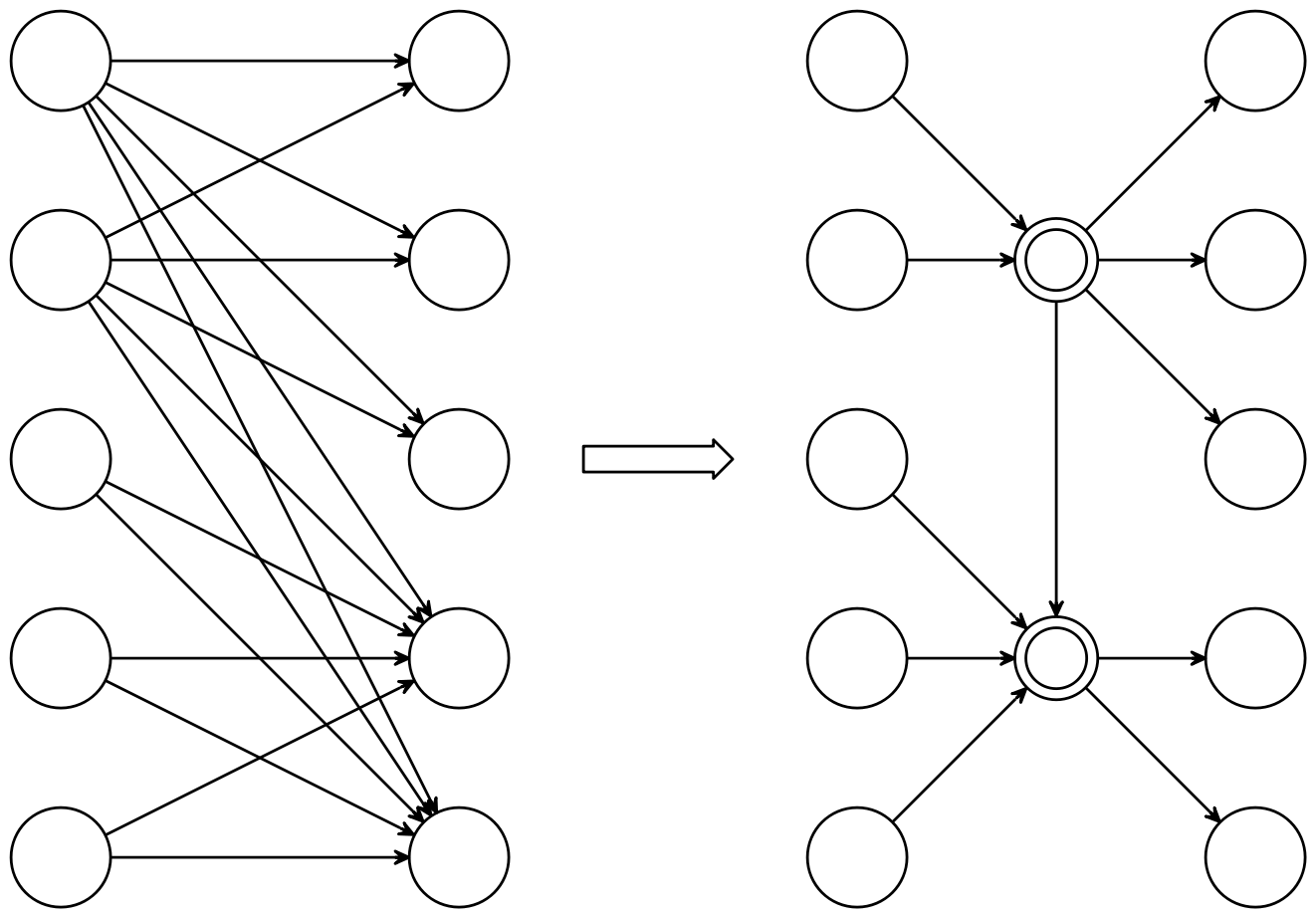
这个优化范围比较广,也没有固定的模式。前后缀优化可以视作这个的子集。多步拆单步的核心思想就是构造中间状态去“合并”转移,在 dp 设计思路也提到过,在可以单步时,单步往往比断点优。这张图很直观地展现了其原理,很像某些建图优化。
除了对着公式优化外,直接从组合意义出发寻找新增的中间状态也是可以的。
例
CF1736E:称当前轮数取的 $a_i$ 位置为取值点。分析解的结构,某些数字会往前交换使其早贡献,然后在到达取值点后会往后交换跟着走。一定不会取值取到交换导致的 $0$,否则可以少往前交换使答案不劣。
(解 1)$f_{i,j,k}$ 表示取值点在 $i$,取值 $a_j$,目前前面空余的交换轮数为 $k$。一种是 $a_j$ 跟着走,一种是换取值,$f_{i,j,k}\rightarrow f_{i+1,j',k-j'+i+2}(j'>\max(i,j))$。从填表法角度看好优化,只需求出 $f$ 关于 $j$ 的前缀 $\max$ 即可。
(解 2)考虑断点转移,$f$ 的状态类似解 1,$j$ 在取值点 $i$ 开始贡献,但转移直接枚举下一段贡献,$f_{i,j,k}\xrightarrow {(i'-i)a_j}f_{i',j',k-j'+i'+1}(i'>i,j'>j,j'\ge i')$。可以拆贡献后两次前缀 $\max$ 处理,我当时考虑的是令 $g_{i,j,k}$ 表示 $j$ 在取值点 $i$ 最后一次贡献,这样 $f\rightarrow g$ 是枚举 $i'$,$g\rightarrow f$ 是枚举 $j'$,我当时原地化了一下,显得很符合直觉。结果发现这个 $g$ 不就是辅助数组嘛!
这两个解法它的辅助数组都是有组合意义的(解 1 的前缀 $\max$ 就是变选择但不决策,类似于前文里一些整数拆分背包),这就是为什么说直接从组合意义出发寻找新增的中间状态也是可以的。
倍增
倍增优化适用于状态数量与转移轮数(较大)无关的情况,在具体题目中一般体现为“不需要记用了几次”这类。一些典型问题包括各种矩乘、完全背包、某些卷积(哎呀反正是个半群就行)等。也是很入门,不讲例子了。
提几个延伸的东西:
- 我感觉矩乘并算不上 dp 的优化,只是一类 dp 转移的通用刻画方法。真正和 ds 无关的技巧也不多,一个是乘向量优化,即,有多组询问时先预处理每个 $T^{2^i}$,然后二进制分解后逐一乘给向量。例子包括 [NOI2020] 美食节 和 [POI2015] Wycieczki。另一个是对于一些特殊矩乘,可能会抽象过度,实际可以记更少的信息。例如 USACO23OPENPlatinumT1 以及某些 ddp。
- 这类倍增可以解决的 dp 在指数极大时往往能通过分析循环节等找到更优的做法,至少能避免倍增的大 $\log$。例如矩乘可以找特征多项式后线性递推,完全背包可以利用上面提到过的性质先贪心,图上定长最短路可以参考 [互测 2023] 【模板】矩阵快速幂。大的思想就是存在不依靠 dp 的更简单的规律。这些就不讨论了。
- 有一类树上倍增维护 dp 支持多次询问的问题,例如 [NOIP2018 提高组] 保卫王国、[CSP-S 2022] 数据传输,它们实质上是纯 ds 问题,跟这里讲的“倍增”是不同的。一般有记录头尾状态和直接套矩乘两种思路,可以推广到 ddp。这篇文章里不会讲 ddp。可以详见猫锟的 ppt 和 17 年集训队论文,以及任轩笛的 18 年集训队论文。
反正大不了就套 top tree。
例
咕
ds 维护 dp 数组
对于一类状态过多,但转移有规律可循的 dp,可以使用 ds 维护 dp 数组,本质就是快速维护 dp 转移时的增量。这类优化有很多子类别:
- 原地化(?)。谁说数组不是 ds 呢?众所周知背包问题可以原地转移而不必滚动数组,这实质上是在状态中隐去了一个维度,使同一位置在一些不相交的时段具有不同的含义(注意要与去维/合并状态区分开,它们是不必考虑某一维,而这里说的是不显式记某一维)。这类优化在状态多于转移时有很好的作用。
- 各类线段树维护(注意与线段树优化 dp 区分)。除了基础的在序列上优化外,还有一类所谓整体 dp,也就是树上 dp 中每个节点上要记一个数组,合并儿子时是直接对应位合并然后加少量修改。这可以直接用线段树合并维护。注意这类线段树是可以打 tag 的,如果 tag 对未建出节点无影响,就判一下即可,否则可以 pushdown 时再新建并下放一层,merge 中出现有一方有点但无儿子时视作 base case 即可(我是从(nfls 7.19 秒速五厘米)的非官方解法学到的),这个 trick 又出现在了 [CTT2023] emerald 里。
- 重剖(dsu on tree)与长剖。值得注意的是它们是支持换根 dp 的,只要保证轻儿子要用的子树外 dp 状态数只与该子树的 siz/dep 有关即可。详见 [十二省联考 2019] 希望,
由于太阴间这里就不讲了。
- slope trick。用于 dp 值关于某一维有凸性的一些情况,详见这篇和这篇。
例
- CF1770E:答案可以转化为求每条边贡献的期望,而每条边的贡献只会在它本身交换时变化,因此只需考虑每个时刻每个点为关键点的概率 $p_{u}$,发现转移相当于是将边两端的 $p$ 取平均。这个 dp 实际原地掉了时间维。
- CF1699E:不妨枚举 $\max$,最大化 $\min$。注意到最优拆分的变化次数为 $\sum\sigma(a_i)$,时间能接受,但空间不行。这时如果放弃该思路就无路可走了。考虑维护每个 $a_i$ 当前的最大 $\min$,搞不了,得求出 $f_{m,x}$ 表示最大值 $\le m$ 时数 $x$ 的最优解,如果 $m\mid x$ 则 $f_{m,x}=\max\left(f_{m-1,x},f_{m,x/m}\right)$,否则 $f_{m,x}=f_{m-1,x}$。这就给出了一个可以原地优化的转移数为 $\mathrm{O}(m\log m)$ 的 dp,从小到大扫 $m$,用桶+指针维护最优 $\min$ 即可。
- [IOI2018] 会议:从笛卡尔树角度来看,只需求每个节点的每个前后缀的答案。以前缀为例,左半直接继承,$f_{u,[l_u,u)}=f_{ls_u,[l_u,u)}$;对于 $i>u$,$f_{u,i}=\min(f_{ls_u,u-1}+(i-u+1)h_u,f_{rs_u,i}+(u-l_u+1)h_u)$,这是先继承 $f_{rs_u}$ 全体加,然后与一条直线取 $\min$。固然可以扩展李超树(区间加时不必沿途下方直线),但是考虑到 $f_{rs_u}$ 是递增且差分均 $\le h_u$(直接考虑意义即可),故可以二分取 $\min$ 切换点做到单 $\log$。在线段树上做,继承直接不动即可。
- [NOI2020] 命运:容斥不容斥最后 dp 形式类似,这里以容斥为例。如果强制钦定一条链全 $0$,那从树形 dp 角度相当于限制了当前点到根最深的 $1$ 的深度上界。把该限制对应的维度用线段树维护,在一条链的底部,选该链就相当于区间求和后减到 $dep_{top}$ 上;两树合并相当于 $\min$ 卷积,可以线段树合并时记一个后缀和。
- CF1534G:顺时针转 $45^\circ$,一个土豆一定在到达对应横坐标时种。dp 状态就记录当前坐标,每次跳到下一个有土豆的横坐标,这个转移相当于与长为 $\Delta x$ 的水平线段作闵可夫斯基和;加土豆相当于全体加上 $\lvert y-C\rvert$。归纳即可证凹。这题涉及斜率区间加和斜率交界点区间位移,线段树无法胜任,可以用平衡树。特殊地,由于只会延长壳的底部,故可以把谷两边的斜率交界点分开维护,用堆就行。
其他. CF671D
ds 优化 dp 转移
这类优化没有通用的方法,得结合具体 dp 方程来看。多步拆单步优化也算属于这个。
注意复杂的 ds 优化 dp 题在填表和刷表时会有较大区别,都要试一下。
ds 优化 dp 转移有一个重要的子集,是决策单调性优化,这里详细讲一下。
决策单调性
所谓决策单调性就是决策点有单调性的 dp。对于在线形式的 dp,如果仅有决策单调性,那应该是无法优化的,必须具有更强的性质(参见 4)。
- 单调队列/单调栈优化。一般从“没前途”角度考虑。略。
- 二分求决策点。只有在转移值严格单峰时才能用,较少见。
- 斜率优化。斜率优化有两种等价形式,分别是将其中一方视作直线/点,另一方视作一个横坐标/去切的斜率。当转移方是静态或加入具有单调性时,可以直接用单调队列/单调栈维护凸壳,否则需要用平衡树或李超树维护。值得注意的是,并非只有 $f_i=\min/\max\{k_ik_j+b_j\}$ 形式可以优化,有些特殊形式的具有较强“没前途”性质的 dp 也可以,详见 [NOI2016] 国王饮水记。另外这类利用”没前途“性质排除转移的 dp 应该能推广到凸壳外的其他结构(例如曼哈顿距离下的凸壳等等),参考 [互测 2023] Grievous Lady。我不是很会。
四边形不等式优化。有三个形式:
- $f_{i,j}=\min_{k=i}^{j-1}\{f_{i,k}+f_{k+1,j}\}+w_{i,j}$。若 $w$ 满足 QI,且 $\forall a\le b\le c\le d,w_{a,d}\le w_{b,c}$,则 $f$ 也满足 QI,且 $p_{i,j-1}\le p_{i,j}\le p_{i+1,j}$,可以按区间长度从小到大转移,三次方变两次方。
- $f_{i,j}=\min_{k=0}^{j-1}\{f_{i-1,k}+w_{k,j}\}$。若 $w$ 满足 QI,则 $f$ 也满足类 QI,且 $p_{i-1,j}\le p_{i,j}\le p_{i,j+1}$,可以类似形式 1 转移,也可以利用分治(对于一个 $i$,先求 $p_{i,n/2}$),都是减一次方。这里计算单点 $w$ 可以暴力移指针。
- $f_i=\min_{j=0}^{i-1}\{f_j+w_{j,i}\}$。若 $w$ 满足 QI,则 $p_i\le p_{i+1}$,且对于 $i
其中后两个情况的 $\log$ 是可以去掉的,详见冯哲的 17 年集训队论文。
- 闵可夫斯基和以及其他与凸性相关的东西。
例
CF1830F:(解 1)$f_i$ 表示最后一个选点 $i$,填表:记 $c_{i,j}$ 表示 $l\le j\le r
(解 2)状态同解 1,刷表:希望对于一个 $j$,一次性更新所有的 $i$,因此对于所有 $i$,维护解 1 中的 $c$,如果它不变,那相当于一个序列,每次与一条直线取 $\max$;但随着 $j$ 的移动,这些 $c$ 可能会区间加减,但原先更新的又不能变。相当于要维护一个取值点会变的李超树,由于 $c_{i,j}$ 关于 $i$ 递增,故可以用扩展李超树维护。
(解 3)倒过来考虑,填表:记 $c_{i,j}$ 表示 $j
CF1720D2:一个 $i$ 从所有 $ja_j\oplus i$ 转移,无法直接 trie 树优化。如果是 $=$ 则可以变成 $a_i\oplus i=a_j\oplus j$。考虑硬套 trie 树,当 $a_i\oplus i$ 在上面走时,比如从一个点走到一个儿子,那在另一个儿子子树中的 $j$ 应当恰好有“一半”可以转移,这样的 $j$ 满足 $j$ 与 $a_i$ 的当前位相同。因此每个节点只需记两类值即可。这种同时与异或和偏序相关的问题可以魔改 trie 树,类似的套路出现在 [NOI Online 2021 提高组] 岛屿探险。
CF1603D:易证只需考虑 $k\le\log n$。$f_{i,j}$ 表示考虑到 $x_i=j$ 的答案。
(解 1)注意到所有 $c(*,j-1)\rightarrow c(*,j)$ 是 $\sigma(j)$ 段区间加。因此用线段树维护所有 $f_{i-1,k}+c(k,j)$ 即可 $\log^3$。
(解 2)$c(l,r)=\sum_{g=l}^rS(r/g)$,其中 $S(n)$ 为 $\varphi$ 的前缀和。注意到 $\forall\,l_1\le l_2\le r_1\le r_2,c(l_1,r_2)+c(l_2,r_1)-c(l_1,r_1)-c(l_2,r_2)=\sum_{g=l_1}^{l_2-1}(S(r_2/g)-S(r_1/g))\ge 0$,故可以套四边形不等式的分治做法。求 $c$ 的方法,注意到可以 $\mathrm{O}(1)$ 移动左端点,均摊 $\mathrm{O}(\log n)$ 移动右端点,而分治做法中左右端点移动在 $1\sim n$ 上求值次数是均匀的,故是 $\log^3$ 的。另一个常数较小的做法是先整除分块求出某个 $c(?,mid)$,再只移左端点。
[NOI2016] 国王饮水记:转移方程形如 $f'_i=\max_{j
决策单调性的证明似乎网上的题解都有问题。考虑 $j'
[Tsinghua Bootcamp 2023 Qualification Round] L. Fence Decoration(给定 $x_{1\cdots n},c_{1\cdots n},d_{1\cdots m}$,$x$ 递增,选择 $x$ 的子序列下标 $p_{1\cdots k}(p_1=1,p_k=n)$,最大化 $\sum_i\sum_j\lvert x_{p_{i+1}}-x_{p_i}-d_j\rvert-\sum_ic_{p_i}$):dp 是 $f_i=\max_{j
(解 1)注意到,两个可选项对应的凸壳只在至多一处相交(因为是全等的),这就可以用李超树维护。
(解 2)由于琴生不等式,转移的代价有四边形不等式,但是这里是 $\max$,也就是对于 $i
其他. CF1067D
cdq 分治
这里指的是四边形不等式以外的 cdq 分治优化转移。对于复杂的断点转移问题,有时可以用 cdq 分治,求出转移和被转移双方与当前 mid 的关系,再借助 ds 优化转移。有些类似于多步拆单步的变形。
这类题较罕见,我目前只遇到过两道。
例
CF1175G:先写出暴力 dp:记 $mx_{l,r}=\max_{i=l}^r\{a_i\}$,则 $f_{i,j}=\min_{k
(解 1)填表。用栈维护 $mx$ 相同的段 $s$,每段的 $mx_s$ 会永远相同但会变,最优解形如 $opt_s=\min\{f_k-k\cdot mx_s\}$,维护其凸壳,支持合并,可以用李超树(也可以用单调队列之类的,启发式合并)。转移考虑每段,形如 $\max_s\{opt_s+mx_s\cdot j\}$,要维护一个大的凸壳,支持加直线和撤销上一次加入,可以用可持久化李超树。
(解 2)利用笛卡尔树结构固定 $\max$。在点 $j$ 处求 $f_j$ 并将其挂到点 $j+1$ 上,这样所有的转移就形如:对于一个点 $u$,求出 $\min_{v\in\mathrm{lsub}_u\cup\{u\}}\{f_{v-1}-(v-1)a_u\}$,并将它更新给 $\mathrm{rsub}_u$,或者说,将该值记为 $g_u$,每次求 $\min_{v\in\mathrm{anc}_u}\{g_v+a_v\cdot u\}$。这个和解 1 本质上是相同的。
(解 3)cdq 分治。直接扫 $[mid+1,r]$ 之间的每个位置转移还是不行的,这里关键要利用 $mid$。如果 $\max$ 选在左半段,那么被转移点只能从左半段的一个前缀转移,从右往左扫被转移点 $j$,维护可选前缀(只增不减)的凸壳,转移形如 $\min_{l\le k\le p}\{f'_k+mx_k\cdot j\}$,由于 $mx$ 只减不增,故可以直接栈维护。如果 $\max$ 选在右半段,类似地从左往右扫被转移点 $j$,维护可选后缀的凸壳,转移形如 $\min_{mid\ge k\ge p}\{f_k-k\cdot mx_j\}$,还是可以用栈维护。注意这里不是用队列维护的原因是,加线和最优取值删线是同侧的。这个写起来比前两种简单很多。
CF771E:(解 2)考虑断点转移,dp 状态只记录跨行矩形的尾。在 $i$ 时枚举 $j>i$,先贪心放一堆行内矩形到 $j$,再从 $j$ 往后放一个跨行矩形。直接转移会平方,考虑 cdq 分治优化,$i$ 在 $mid$ 之前,$j$ 在 $mid$ 之后。两边可以分别以 $mid$ 为边界贪心向右/向左跳,然后考虑跨 $mid$ 的行内矩形,共四种情况。有跨 $mid$ 的矩形就左边再贪心跳一次,这样就转化成一次全体更新,两次一维偏序,一次二维偏序。$\mathrm{O}(n\log^2n)$。
有后效性 dp 的处理
对于最优化问题,如果所有转移的起点只与一个 dp 值相关,那就是最短路,否则我也不会。计数问题要么魔改高斯消元,要么手玩方程。
有些比较诡异的题。
例
其他. CF865C、[THUPC 2023 初赛] 最后的活动、+CF1778D、+CF1667E、(字符串)
参考文章
- 邓明扬,《杂题选讲》,WC2022 讲课。
- 《一类动态规划选讲》。
- Alex_Wei,《DP 优化方法大杂烩》,https://www.cnblogs.com/alex-wei/p/DP_Involution.html & https://www.cnblogs.com/alex-wei/p/DP_optimization_method_II.html。
- OI-Wiki,《四边形不等式优化》,https://oi-wiki.org/dp/opt/quadrangle/。
- @changruinian2020 给予我的指示。
- @linrui 与我讨论的一些题目和思路。
一些例题参考了各处的题解,但是基本都是我先自己想出来的。如果是后来发现的一些他人独创的解法我都标出来了,如果您觉得漏标了可以提醒我。








 鲁ICP备2025150228号
鲁ICP备2025150228号