本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2025-09-18 14:18:14

Statement

给定一个 $n \times m$ 的矩形，包含 $nm$ 个方格，给定一个正整数 $k$。

有一部分格子包含目标。

现在需要选择一个位置 $(x,y)$，以及一个方向（可选范围：右下，右上，左上，左下）。选中之后，选中方向内所有与 $(x,y)$ 曼哈顿距离不超过 $k$ 的格子内的目标均被击中。

提示：$k=3$ 可能击中的区域的形态如下：

$n\times m \le 10^5,k \le 10^5$。

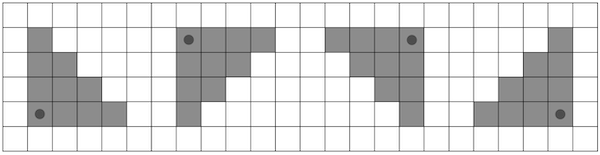
首先 $4$ 种方向如果分类讨论难度会上天。

此时注意到，任意一种合法的操作，均可以通过旋转矩形，对应到另一个方向的某个合法操作。

同时旋转矩形后执行的任意合法操作，总是等价于旋转前的某一个合法操作。

所以，可以仅保留一种选择方向，对矩形的 $4$ 种旋转方式分别计算答案取最大值就可以了。

此处选择什么方向无所谓，我在此以右上方向（即第一张图片）为例。

由于选择区域的形状比较特别，目标总数量难以直接通过前缀和等方式快速得到，所以考虑递推。

令 $w(i,j)$ 表示以 $(i,j)$ 为左下角的区域的目标总数。

考虑其和 $w(i-1,j)$ 的关系。

对于 $k=3$ 大概是下面的样子：

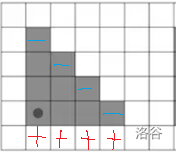
红色加号代表新增区域，蓝色减号代表减少的区域。

可以发现增加的红色区域是第 $i$ 行的 $j \sim j+k$ 列。

减少的蓝色区域是 $(i-1,j+k)$ 为结尾，$(i-k-1,1)$ 为开始的对角线。

那么对每一行预处理从左到右的前缀和，以及预处理左上到右下的对角线前缀和，就可以 $O(1)$ 从 $w(i-1,j)$ 转化到 $w(i,j)$ 了。