本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2024-02-27 19:31:47

A:

Doremy's Perfect Math Class

题面翻译

给定一个正整数集合 $S$。对于 $S$，你可以执行以下操作若干次：

• 从集合中选两个数 $x$ 和 $y$，使得 $x$ 和 $y$ 满足 $x>y$ 并且 $x-y$ 不在集合 $S$ 中。
• 将 $x-y$ 作为一个新元素加入到集合中。

假设操作方式是最优的，输出到无法操作时集合 $S$ 的最大长度。题目保证结果有限。

题目描述

"Everybody! Doremy's Perfect Math Class is about to start! Come and do your best if you want to have as much IQ as me!" In today's math class, Doremy is teaching everyone subtraction. Now she gives you a quiz to prove that you are paying attention in class.

You are given a set $ S $ containing positive integers. You may perform the following operation some (possibly zero) number of times:

• choose two integers $ x $ and $ y $ from the set $ S $ such that $ x > y $ and $ x - y $ is not in the set $ S $ .
• add $ x-y $ into the set $ S $ .

You need to tell Doremy the maximum possible number of integers in $ S $ if the operations are performed optimally. It can be proven that this number is finite.

输入格式

The input consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1\le t\le 10^4 $ ) — the number of test cases. The description of the test cases follows.

The first line contains an integer $ n $ ( $ 2 \le n\le 10^5 $ ) — the size of the set $ S $ .

The second line contains $ n $ integers $ a_1,a_2,\dots,a_n $ ( $ 1\le a_1 < a_2 < \cdots < a_n \le 10^9 $ ) — the positive integers in $ S $ .

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2\cdot 10^5 $ .

输出格式

For each test case, you need to output the maximum possible number of integers in $ S $ . It can be proven that this value is finite.

样例 #1

样例输入 #1

2
2
1 2
3
5 10 25

样例输出 #1

2
5

提示

In the first test case, no such $ x $ and $ y $ exist. The maximum possible number of integers in $ S $ is $ 2 $ .

In the second test case,

• $ S=\{5,10,25\} $ at first. You can choose $ x=25 $ , $ y=10 $ , then add $ x-y=15 $ to the set.
• $ S=\{5,10,15,25\} $ now. You can choose $ x=25 $ , $ y=5 $ , then add $ x-y=20 $ to the set.
• $ S=\{5,10,15,20,25\} $ now. You can not perform any operation now.

After performing all operations, the number of integers in $ S $ is $ 5 $ . It can be proven that no other sequence of operations allows $ S $ to contain more than $ 5 $ integers.

B:

Prime Square

题面翻译

定义一个$n\times n$素数正方形为:

• 所有的数不大于$10^5$
• 所有的数不是质数
• 每行、每列的和都是质数

输入$n$，输出大小为$n$的素数正方形

翻译 by jun头吉吉

题目描述

Sasha likes investigating different math objects, for example, magic squares. But Sasha understands that magic squares have already been studied by hundreds of people, so he sees no sense of studying them further. Instead, he invented his own type of square — a prime square.

A square of size $ n \times n $ is called prime if the following three conditions are held simultaneously:

• all numbers on the square are non-negative integers not exceeding $ 10^5 $ ;
• there are no prime numbers in the square;
• sums of integers in each row and each column are prime numbers.

Sasha has an integer $ n $ . He asks you to find any prime square of size $ n \times n $ . Sasha is absolutely sure such squares exist, so just help him!

输入格式

The first line contains a single integer $ t $ ( $ 1 \le t \le 10 $ ) — the number of test cases.

Each of the next $ t $ lines contains a single integer $ n $ ( $ 2 \le n \le 100 $ ) — the required size of a square.

输出格式

For each test case print $ n $ lines, each containing $ n $ integers — the prime square you built. If there are multiple answers, print any.

样例 #1

样例输入 #1

2
4
2

样例输出 #1

4 6 8 1
4 9 9 9
4 10 10 65
1 4 4 4
1 1
1 1

C:

Numbers on Whiteboard

题面翻译

$T$ 次询问，对于每一次询问：

给定 $n$ 个数，为 $1,2,3,...,n$，每次可以选择两个数 $a,b$ 并删除，然后把 $\left\lceil\frac{a+b}{2}\right\rceil$ 加入到这些数中。最小化最后剩下的一个数，输出这个数并且输出构造方案。

$2\leq n\leq 2\cdot10^5,\sum n \leq 2\cdot10^5$

题目描述

Numbers $ 1, 2, 3, \dots n $ (each integer from $ 1 $ to $ n $ once) are written on a board. In one operation you can erase any two numbers $ a $ and $ b $ from the board and write one integer $ \frac{a + b}{2} $ rounded up instead.

You should perform the given operation $ n - 1 $ times and make the resulting number that will be left on the board as small as possible.

For example, if $ n = 4 $ , the following course of action is optimal:

1. choose $ a = 4 $ and $ b = 2 $ , so the new number is $ 3 $ , and the whiteboard contains $ [1, 3, 3] $ ;
2. choose $ a = 3 $ and $ b = 3 $ , so the new number is $ 3 $ , and the whiteboard contains $ [1, 3] $ ;
3. choose $ a = 1 $ and $ b = 3 $ , so the new number is $ 2 $ , and the whiteboard contains $ [2] $ .

It's easy to see that after $ n - 1 $ operations, there will be left only one number. Your goal is to minimize it.

输入格式

The first line contains one integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases.

The only line of each test case contains one integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of integers written on the board initially.

It's guaranteed that the total sum of $ n $ over test cases doesn't exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, in the first line, print the minimum possible number left on the board after $ n - 1 $ operations. Each of the next $ n - 1 $ lines should contain two integers — numbers $ a $ and $ b $ chosen and erased in each operation.

样例 #1

样例输入 #1

1
4

样例输出 #1

2
2 4
3 3
3 1

D:

Paint the Array

题面翻译

$T$ 组数据。

对于每组数据，给定一个长度为 $n$ 的序列。

问是否存在一个数 $d$ ，将所有能被 $d$ 整除的数标记为红色，所有不能被 $d$ 整除的数标记为蓝色，使得序列中没有相邻的元素具有相同的颜色。

若存在，则输出任意一个满足条件的 $d$ ；若不存在，则输出 $0$ 。

题目描述

You are given an array $ a $ consisting of $ n $ positive integers. You have to choose a positive integer $ d $ and paint all elements into two colors. All elements which are divisible by $ d $ will be painted red, and all other elements will be painted blue.

The coloring is called beautiful if there are no pairs of adjacent elements with the same color in the array. Your task is to find any value of $ d $ which yields a beautiful coloring, or report that it is impossible.

输入格式

The first line contains a single integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of testcases.

The first line of each testcase contains one integer $ n $ ( $ 2 \le n \le 100 $ ) — the number of elements of the array.

The second line of each testcase contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 10^{18} $ ).

输出格式

For each testcase print a single integer. If there is no such value of $ d $ that yields a beautiful coloring, print $ 0 $ . Otherwise, print any suitable value of $ d $ ( $ 1 \le d \le 10^{18} $ ).

样例 #1

样例输入 #1

5
5
1 2 3 4 5
3
10 5 15
3
100 10 200
10
9 8 2 6 6 2 8 6 5 4
2
1 3

样例输出 #1

2
0
100
0
3

E:

Snow Walking Robot

题面翻译

有一个机器人，站在一个平面直角坐标系上，开始时他的坐标为$(0,0)$

给出一个指令序列$s$，它只由L,R,U,D 四个大写字母组成
若机器人当前坐标为$(x,y)$

• 如果当前字母为 L，那么机器人就会向左移动到$x-1,y$
• 如果当前字母为 R，那么机器人就会向右移动到$x+1,y$
• 如果当前字母为 U，那么机器人就会向上移动到$x,y+1$
• 如果当前字母为 D，那么机器人就会向下移动到$x,y-1$

如果一个坐标的点被走过了两次（除$(0,0)$外），那么机器人就会爆炸
一个操作序列合法，当且仅当中途机器人不会爆炸，并且满足指令序列结束时，机器人的坐标为$(0,0)$（也就是最后回到原点）
当然，空指令序列也是合法的

我们发现，所有的指令序列不一定都合法

给出一个指令序列$s$，你的任务是通过删除指令和重排序列，让指令序列合法，并且满足删除的指令数最小

输入格式

第一行一个整数$q$，表示有$q$组数据

接下来$q$行，每行一个字符串，代表一个指令串

输出格式

对于每组数据： 第一行一个整数，表示最多剩下多少条指令，使得指令序列合法，如果无论如何都不合法，输出$0$
第二行表示合法的指令序列，如果有多个合法序列，输出任意一个
如果无论如何都不合法，输出空的一行（注意那一行要空出来，详情见样例）

数据范围

$1 \le q \le 2\cdot 10^4$，$\sum|s| \le 10^5$
其中$|s|$为字符串$s$的长度
感谢 @_Wolverine 提供的翻译

题目描述

Recently you have bought a snow walking robot and brought it home. Suppose your home is a cell $ (0, 0) $ on an infinite grid.

You also have the sequence of instructions of this robot. It is written as the string $ s $ consisting of characters 'L', 'R', 'U' and 'D'. If the robot is in the cell $ (x, y) $ right now, he can move to one of the adjacent cells (depending on the current instruction).

• If the current instruction is 'L', then the robot can move to the left to $ (x - 1, y) $ ;
• if the current instruction is 'R', then the robot can move to the right to $ (x + 1, y) $ ;
• if the current instruction is 'U', then the robot can move to the top to $ (x, y + 1) $ ;
• if the current instruction is 'D', then the robot can move to the bottom to $ (x, y - 1) $ .

You've noticed the warning on the last page of the manual: if the robot visits some cell (except $ (0, 0) $ ) twice then it breaks.

So the sequence of instructions is valid if the robot starts in the cell $ (0, 0) $ , performs the given instructions, visits no cell other than $ (0, 0) $ two or more times and ends the path in the cell $ (0, 0) $ . Also cell $ (0, 0) $ should be visited at most two times: at the beginning and at the end (if the path is empty then it is visited only once). For example, the following sequences of instructions are considered valid: "UD", "RL", "UUURULLDDDDLDDRRUU", and the following are considered invalid: "U" (the endpoint is not $ (0, 0) $ ) and "UUDD" (the cell $ (0, 1) $ is visited twice).

The initial sequence of instructions, however, might be not valid. You don't want your robot to break so you decided to reprogram it in the following way: you will remove some (possibly, all or none) instructions from the initial sequence of instructions, then rearrange the remaining instructions as you wish and turn on your robot to move.

Your task is to remove as few instructions from the initial sequence as possible and rearrange the remaining ones so that the sequence is valid. Report the valid sequence of the maximum length you can obtain.

Note that you can choose any order of remaining instructions (you don't need to minimize the number of swaps or any other similar metric).

You have to answer $ q $ independent test cases.

输入格式

The first line of the input contains one integer $ q $ ( $ 1 \le q \le 2 \cdot 10^4 $ ) — the number of test cases.

The next $ q $ lines contain test cases. The $ i $ -th test case is given as the string $ s $ consisting of at least $ 1 $ and no more than $ 10^5 $ characters 'L', 'R', 'U' and 'D' — the initial sequence of instructions.

It is guaranteed that the sum of $ |s| $ (where $ |s| $ is the length of $ s $ ) does not exceed $ 10^5 $ over all test cases ( $ \sum |s| \le 10^5 $ ).

输出格式

For each test case print the answer on it. In the first line print the maximum number of remaining instructions. In the second line print the valid sequence of remaining instructions $ t $ the robot has to perform. The moves are performed from left to right in the order of the printed sequence. If there are several answers, you can print any. If the answer is $ 0 $ , you are allowed to print an empty line (but you can don't print it).

样例 #1

样例输入 #1

6
LRU
DURLDRUDRULRDURDDL
LRUDDLRUDRUL
LLLLRRRR
URDUR
LLL

样例输出 #1

2
LR
14
RUURDDDDLLLUUR
12
ULDDDRRRUULL
2
LR
2
UD
0

提示

There are only two possible answers in the first test case: "LR" and "RL".

The picture corresponding to the second test case:

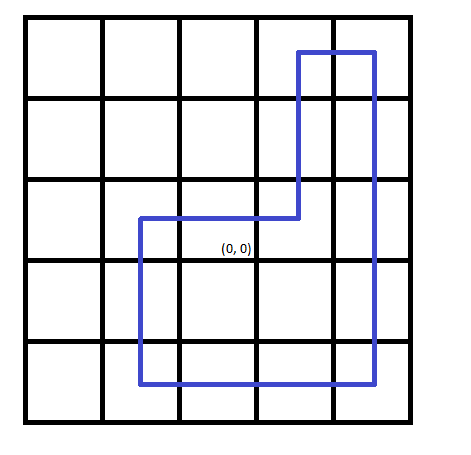Note that the direction of traverse does not matter Another correct answer to the third test case: "URDDLLLUURDR".