本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2025-06-30 20:07:14

CF1401E 严谨证明

本题结论是：分出区域的数量 = 交点数量 $+$ 贯穿边的数量 $+1$，想要感性理解请参考其他题解，这里给出严谨的证明。严谨证明来自 lzx（太强了）。

前置定理部分

在本文中平面图的定义为：可以在一个平面上绘制的无向图，且任何两条边仅在顶点处相交。对于本题也就是说，两条边的交点也被计算为顶点。

下图使用黑色点表示平面图的顶点，左侧不是平面图，右侧是平面图。

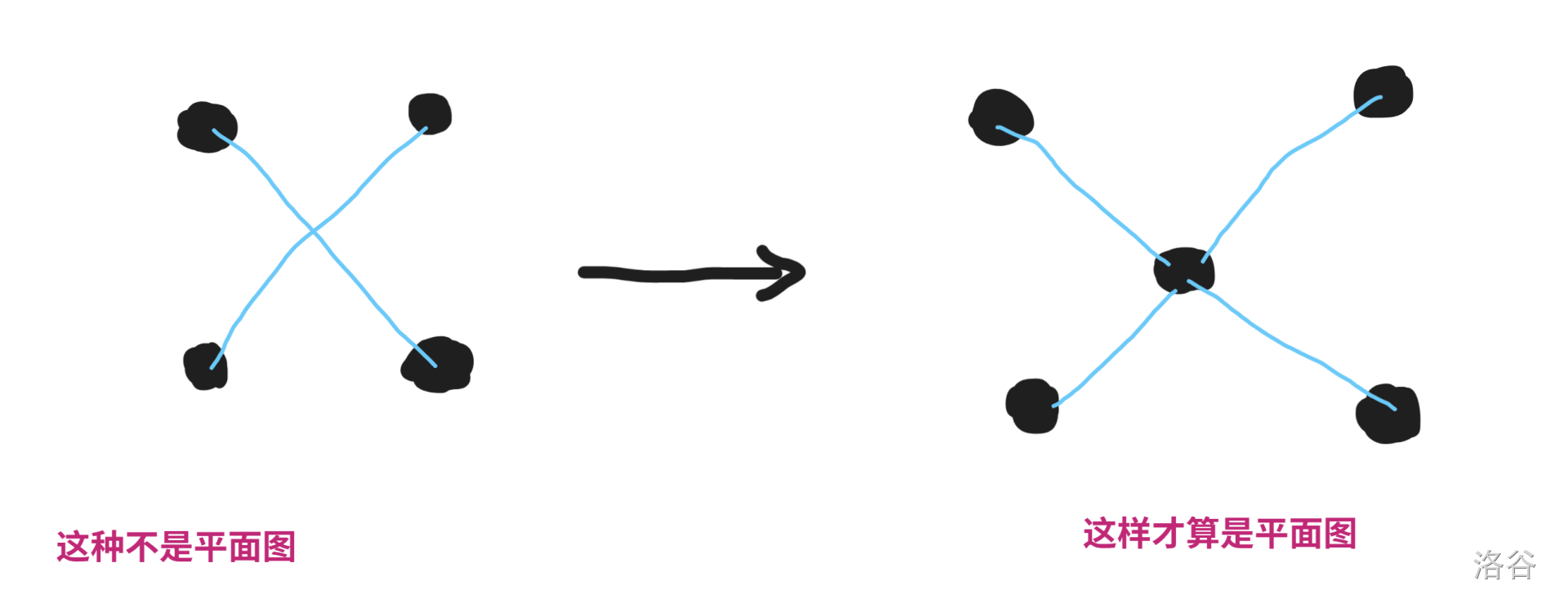
在平面图中，我们设点的数量为 $N$，边的数量为 $M$，所划分成区域的数量为 $K$，要注意这里的 $K$ 不仅包含了图形内部，也包含了外部的区域，例如在下面图中 $K = 2$。

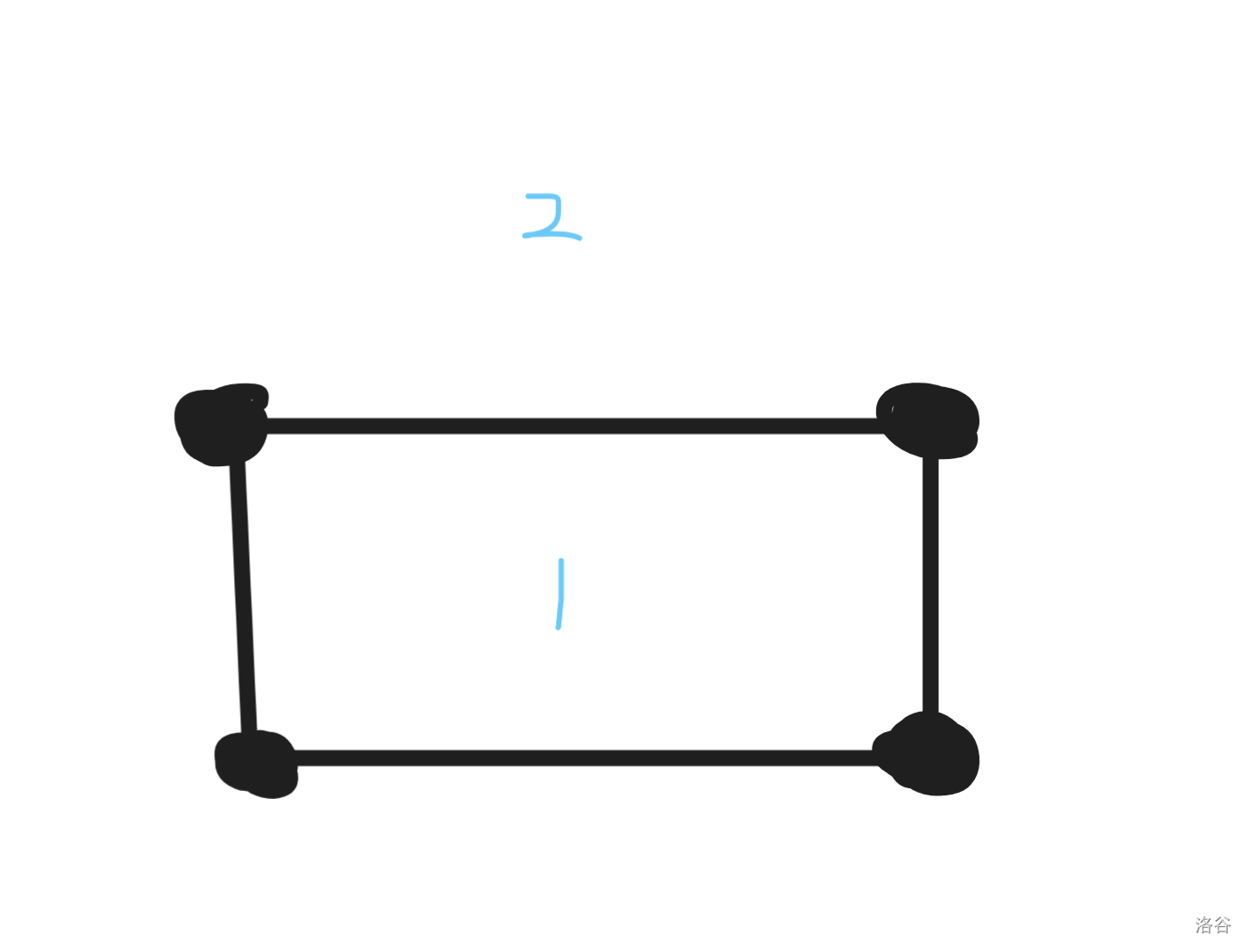
定理内容为：$N - M + K = 2$。

由于 $K$ 还包含了外部区域，这部分不是我们想要统计的，因此在这个题里面，实际上是 $N - M + K = 1$，进行移项，易得 $K = M - N + 1$。

这样我们就把问题转化为，对于给出的这张图，将其转化为一张平面图之后，要求出它的点的数量 $N$ 和边的数量 $M$。

下文中，我们把长度为 $10^6$ 的边称为贯穿边，其余称为普通边，假设贯穿边总共有 $l$ 条，并把交点的个数设为 $x$。

我们分别来计算，先来考虑点的数量，分为矩形上的点和矩形内部的点两部分计算。

对于矩形上的点，有以下几种：

将其相加，位于矩形上的点总共有 $4 + m + l$ 个。

矩形内部的点，也就是交点的个数 $x$。

将上述两部分相加，得到 $N = 4 + m + l + x$。

我们依旧分开考虑，首先来看矩形上的。

最初的矩形有 $4$ 条边，随后往里加入边，发现每加入一条普通边，会与矩形产生一个交点，这个交点把一条边分成了两段，也就相当于每条普通边会额外产生 $1$ 条边。

再来看贯穿边，贯穿边会与矩形产生 $2$ 个交点，也就是将两条线段分别分成 $2$ 段，因此每条贯穿边会产生 $2$ 条边。

矩形上共有 $4 + m + l$ 条边。

接下来看矩形内部，每个交点会产生 $2$ 条边，如下图所示。

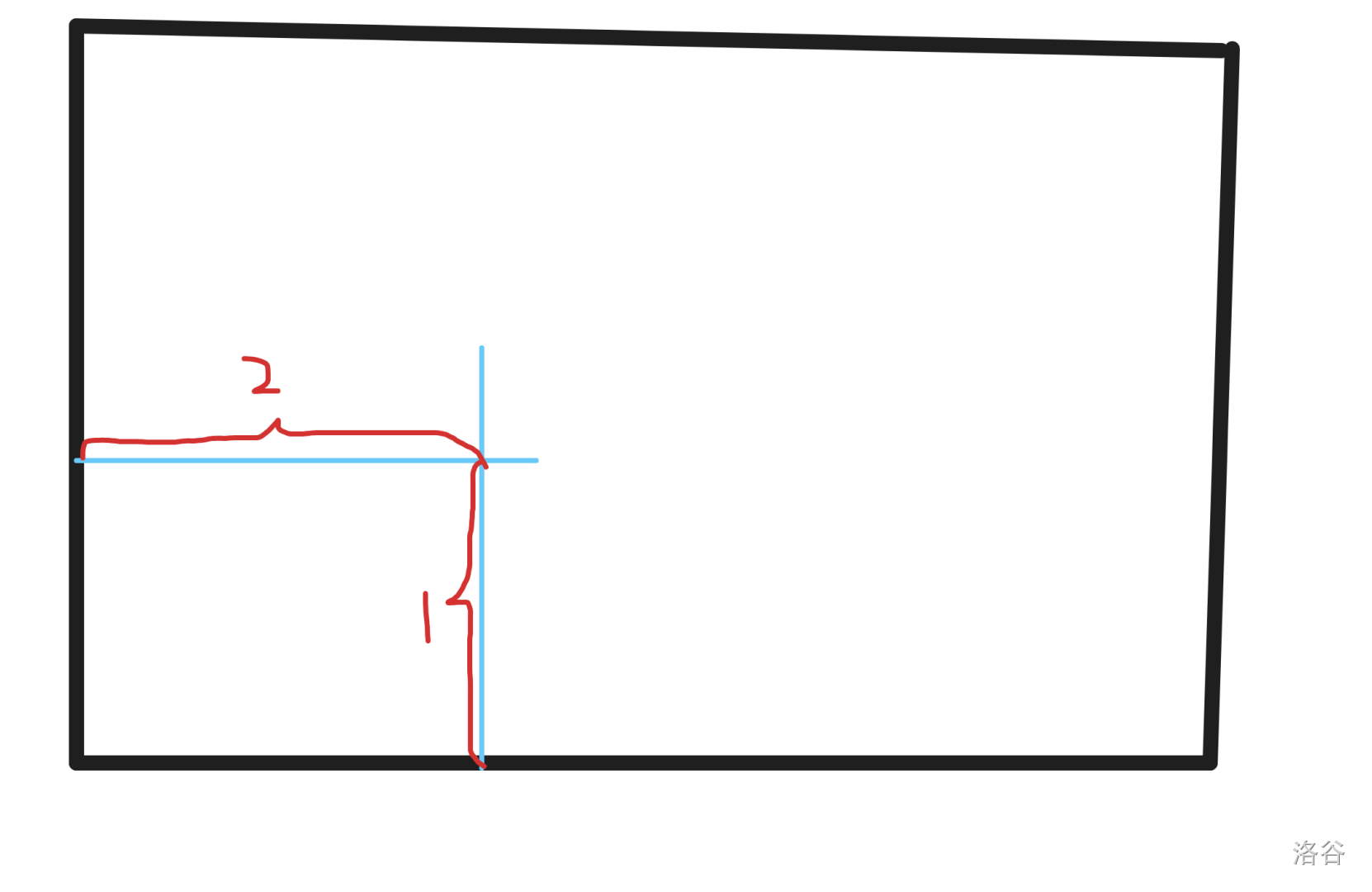
如图，两条普通边产生了 $1$ 个交点，这个交点对应着 $1,2$ 两条边。这里要注意，普通边在末端并没有与矩形另一边相交，因此伸出部分不被算作边，相当于实际上这幅图是这样的。

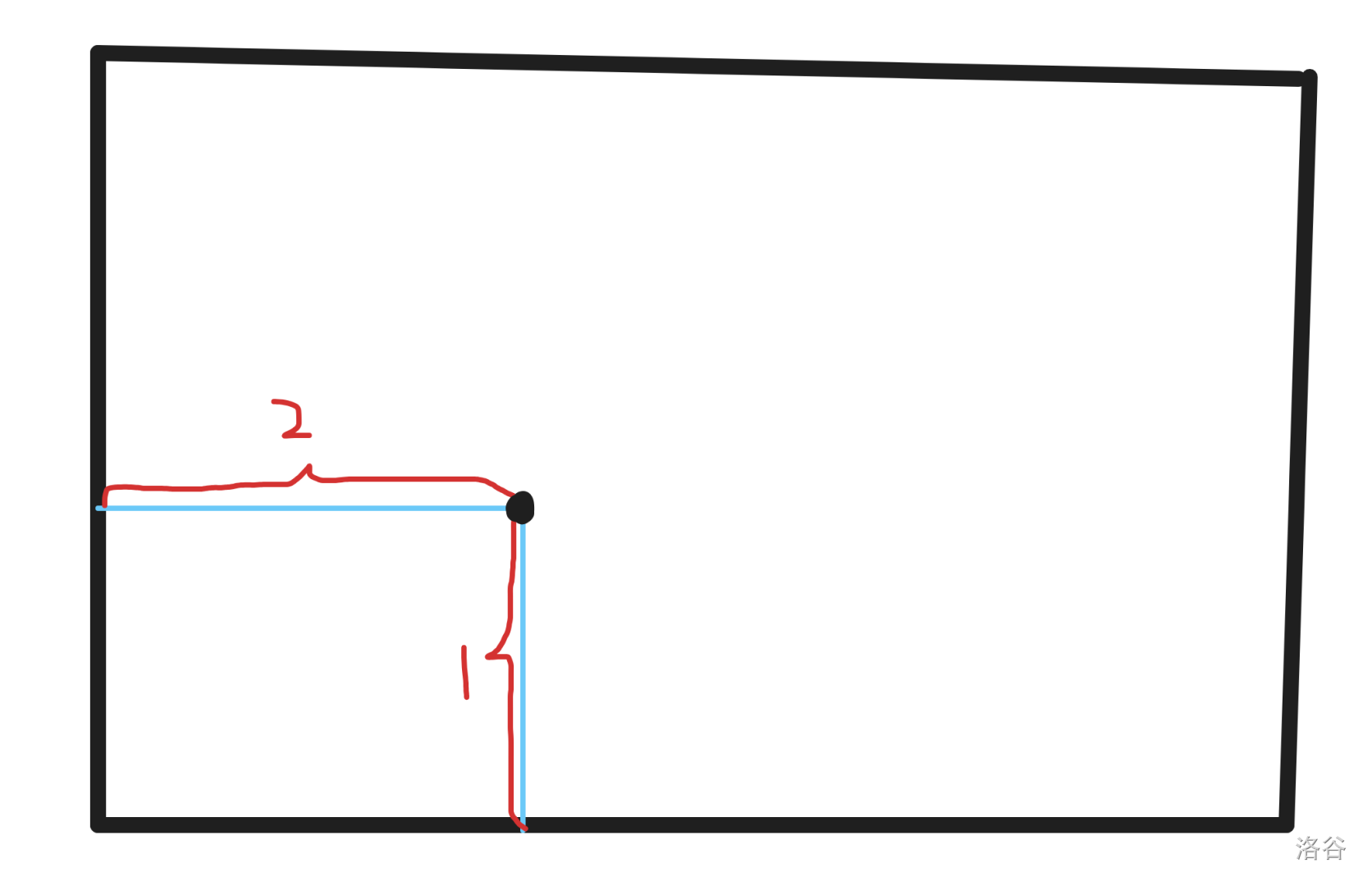
再来看贯穿边，贯穿边的每个交点会产生 $3$ 条边，因此两种边一共会产生 $2 \times x + l$ 的贡献，贯穿边具体如图。

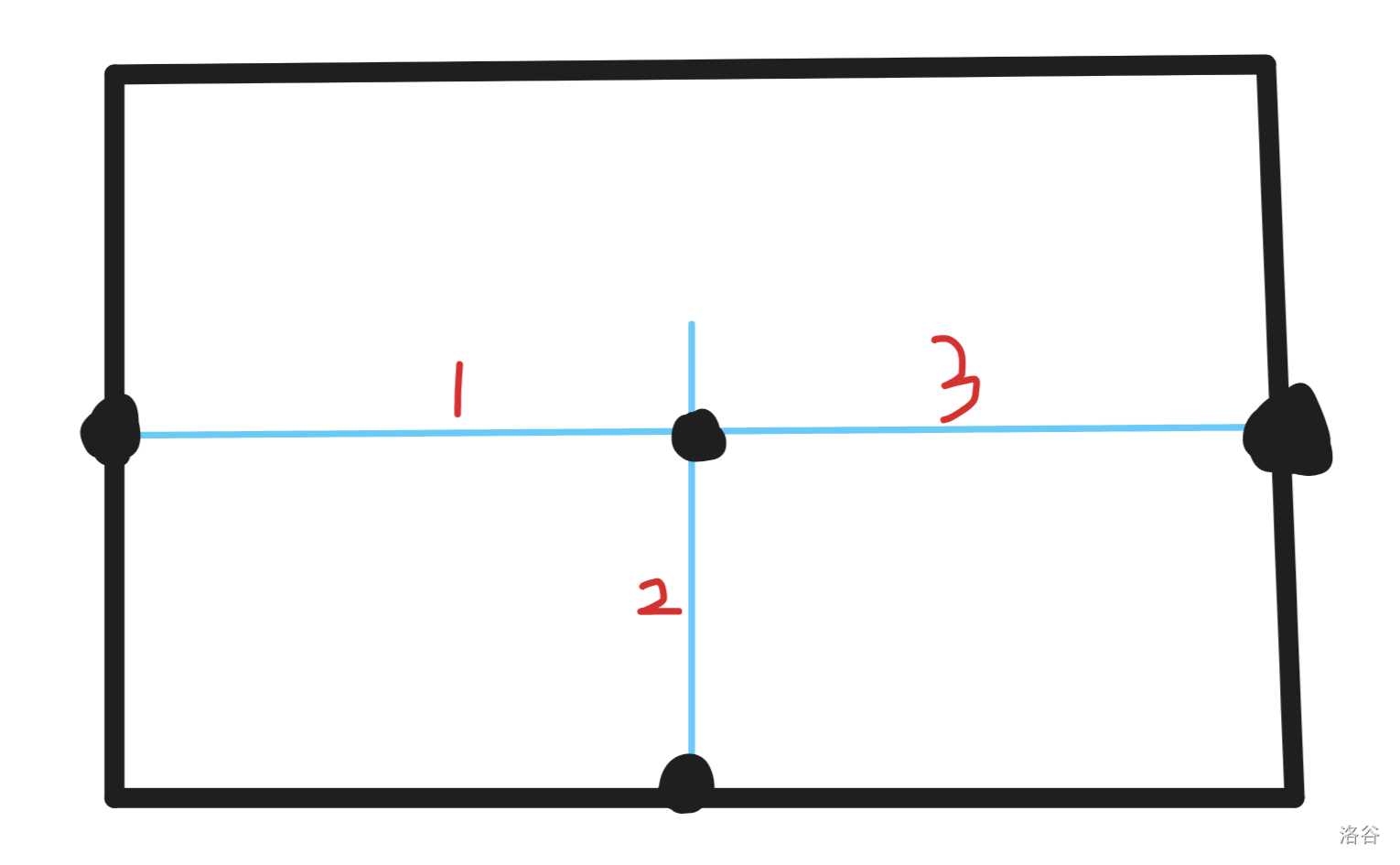
那么边的数量 $M = 4 + m + 2 \times l + 2 \times x$。

我们把 $N,M$ 代回到本题的公式中，$K = M - N + 1 = l + x + 1$，也就是结论，分出的区域数量 $=$ 交点数量 $+$ 贯穿边的数量 $+1$。