本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2024-01-06 17:37:53

思路:

先考虑 $n=2$ 怎么做，以 $n=2,m=3$ 为例：

那么显然可以这么走：

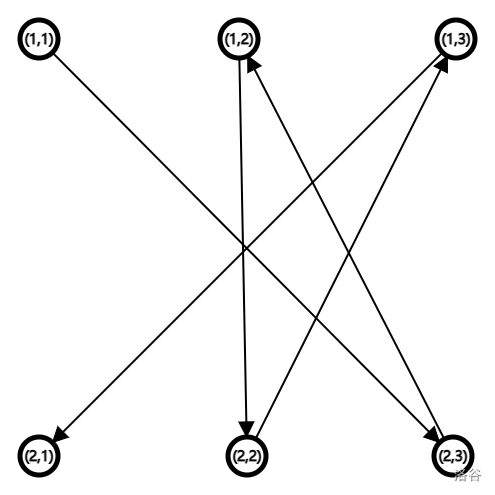
也就是是两边是对称的，所以这些增量都是形如 $(x,y_1),(-x,y_1),\dots$，而每个 $x,-x$ 循环中 $y$ 都不同那么是合法的。

进一步总结得出：

设当前坐标为 $(x, y)$。

• 若当前在上方，那么下一次坐标就是 $(x+1,m-y+1)$
• 若当前在下方，那么下一次坐标就是 $(x+1,m-y)$

而当 $n > 2$ 时，依以 $m=3$ 为例：

有一种走法时这样的：

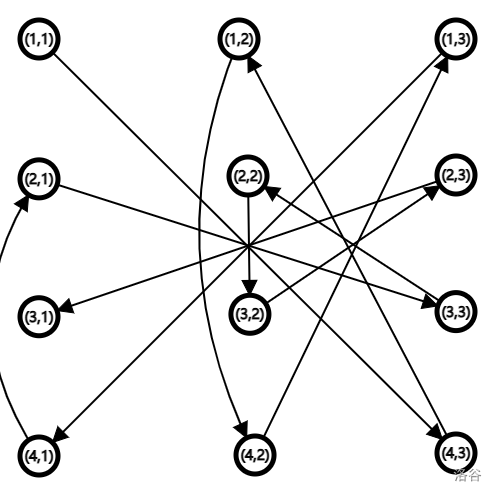
有没有发现什么规律？

首先对于 $(1,n),(2,n-1),\dots$ 这些行对之间仅有一条连边。

如图上 $(1,4)$ 与 $(2,3)$ 这两个行对之间仅有 $(4,1) \to (2,1)$ 这一条边。

然后在每个行对中按照上面总结的做即可。

若最后还剩一行的话，那么可以考虑 $x$ 不变 $y$ 是 $1 \to m \to 2 \to (m -2)\dots$。

然后就做完啦。

Code:

#include <bits\/stdc++.h>

using namespace std;

int n, m;
bool st[1000010];

void dfs(int i, int j) {
	if (i > j) return;
	if (i == j) {
		for (int t1 = m, t2 = 1; t1 >= t2; --t1, ++t2) {
			if (t1 == t2) {
				printf("%d %d\n", i, t1);
			} else {
				printf("%d %d\n", i, t2);
				printf("%d %d\n", i, t1);
			}
		}
	} else {
		for (int dx = 1; dx <= m; ++dx) {
			if (dx == m) {
				printf("%d %d\n", j, m - dx + 1);
				if (i + 1 != j) {
					if (i + 1 != j - 1)
						printf("%d %d\n", i + 1, 1);
					dfs(i + 1, j - 1);
				}
				continue;
			}
			printf("%d %d\n", j, m - dx + 1);
			printf("%d %d\n", i, dx + 1);
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	if (n != 1)
		printf("%d %d\n", 1, 1);
	dfs(1, n);
	return 0;
}