本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2024-11-06 10:10:06

前置知识：

杨表

看到最长上升/下降子序列长度还有计数，考虑杨表。

然后有一个结论，就是杨表的第一行的长度就是这个序列的最长上升子序列的长度，第一列的长度就是这个序列的最长下降子序列的长度。

由于这道题固定了最长上升子序列和最长下降自序的长度，并且长度为 $AB - 1$，那么最后杨表一定是长这个样子的：

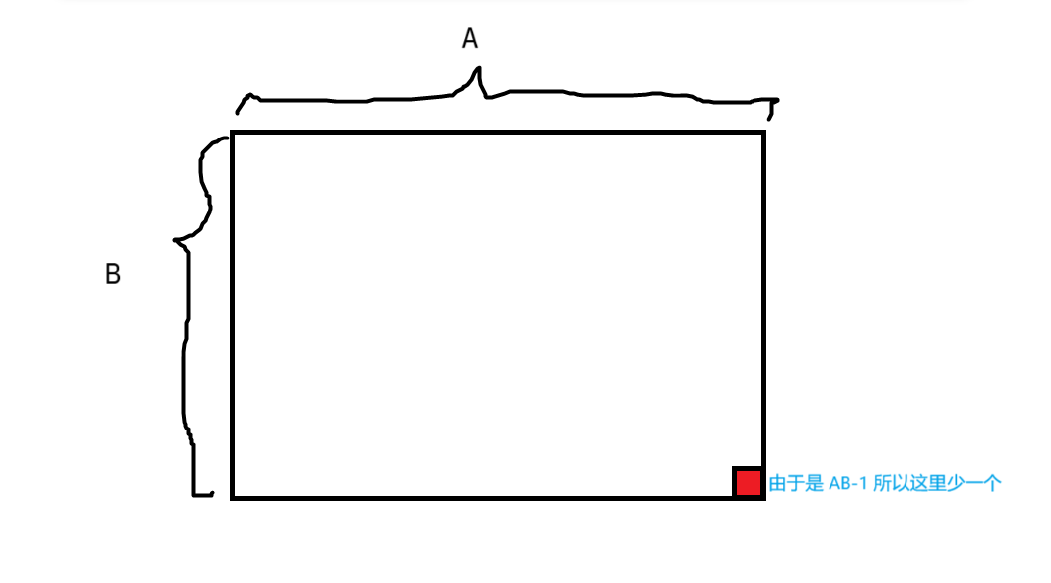
然后由于最后要加上 $n + 0.5$，并且数量不变，所以要把 $n + 0.5$ 扔到 $b_{1,A}$ 上，并且把所以 $b_{i, A} (1 \le i < B)$ 都一一放到 $b_{i, A} (2 \le i \le B)$ 上。

那么我们要满足：

$b_{i + 1, A - 1} < b_{i, A}$，因为这样才能让 $n + 0.5$ 插进去后所有的 $b_{i, A}$ 都到 $b_{i + 1, A}$ 上。

由于数据范围极小，那么我们可以考虑暴力 $DP$。

设 $f_{a_1,a_2, \dots, a_A}$ 表示杨表第 $i$ 列填了 $a_i$ 个数的序列个数。

那么这个直接暴力转移，枚举当前数填到哪里，只要 $a_i < a_{i - 1}$，那么就可以从 $a_1, a_2, \dots, a_i, \dots, a_A$ 转移到 $a_1, a_2, \dots, a_i + 1, \dots, a_A$。

再统计合法的杨表的数量，那么我们设 $f_{a_1, a_2, \dots, a_n}$ 表示满足的杨表个数。

那么我们考虑大部分转移和上一部分是一样的，不过对于 $a_A$，它必须 $< a_{A - 1} - 1$ 才能转移，因为如果是 $< a_{A - 1}$，那么当前这个数填到 $a_A$ 上后，若 $a_A = a_{A - 1}$ 并且 $a_{A - 1}$ 还未填，那么我们就会发现再填上一个数之后就有一个不满足 $b_{i + 1, A - 1} < b_{i, A}$。

然后就做完了。

Code

#include <bits\/stdc++.h>

using namespace std;

int A, B, mod;
map<vector<int>, int> f;

int dp1() {
	f.clear();
	f[vector<int> (A, 0)] = 1;

	for (auto [u, v] : f) {
		vector<int> t = u;
		for (int i = 0; i < A; ++i) {
			int lim = (i == 0) ? (B) : (u[i - 1]);

			if (u[i] < lim) {
				++t[i];

				f[t] += v;
				if (f[t] >= mod) f[t] -= mod;

				--t[i];
			}
		}
	}

	vector<int> t(A, B);
	return f[t];
}

int dp2() {
	f.clear();
	f[vector<int> (A, 0)] = 1;

	for (auto [u, v] : f) {
		vector<int> t = u;
		for (int i = 0; i < A; ++i) {
			int lim = (i == 0) ? B : ((i == A - 1) ? (u[i - 1] - 1) : (u[i - 1]));

			if (t[i] < lim) {
				++t[i];

				f[t] += v;
				if (f[t] >= mod) f[t] -= mod;

				--t[i];
			}
		}
	}

	vector<int> t(A, B);
	t[A - 1] = B - 1;

	return f[t];
}

int main() {
	scanf("%d%d%d", &A, &B, &mod);

	int res1 = dp1();
	cout << res1 << endl;
	int res2 = dp2();

	printf("%d\n", 1ll * res1 * res2 % mod);

	return 0;
}

当然，我们也可以先在第 $A$ 列选一个（也就是 $n + 0.5$ 的位置），然后再填其他的，这样也是可以的。

这里只给出和上一个方法不同的地方。

Code:

int dp2() {
	f.clear();
	vector<int> a(A, 0);
	a.back() = 1;
	f[a] = 1;

	for (auto [u, v] : f) {
		vector<int> t = u;
		for (int i = 0; i < A; ++i) {
			int lim = (i == 0) ? B : (u[i - 1]);

			if (t[i] < lim) {
				++t[i];

				f[t] += v;
				if (f[t] >= mod) f[t] -= mod;

				--t[i];
			}
		}
	}

	vector<int> t(A, B);

	return f[t];
}