本文章由 WyOJ Shojo 从洛谷专栏拉取,原发布时间为 2021-11-27 22:58:42
前言:
本博客学习于此篇文章
前置:
点值表示法:
$f(x) = {(x0,f[x0]),(x1,f[x1]).....(xn,f[xn])}$
$g(x) = {(x0,g[x0]),(x1,g[x1]).....(xn,g[xn])}$
$f(x) * g(x) = {(x0,f[x0]g[x0]),(x1,f[x1]g[x1]).....(xn,f[xn]*g[xn])} $
快速傅里叶变换中的特殊性质:
设 $F(x)$ 为快速傅里叶变换函数,那么:
$F(f(x)*g(x)) = F(f(x)) * F(g(x))$
也就是通过两个函数的卷积的进行FFT得到的结果 $=$ 分别对两个函数进行FFT后的值相乘 。
复数:
复数由实数和虚数两个部分组成,其中实数部分可以看作横轴上的数,虚数部分可以看作纵轴上的数,同时也用另一个单位 $i$ 作为虚数的单位。 $i$ 满足 $i = \sqrt{-1}$,也就是 $i^{2} = -1$。
设一个复数的实数部分为a,虚数部分为b,那么它的模记为 $| x |$。模:指的就是一个复数到达原点的距离(相当于复数的绝对值),此时可以发现直接使用距离公式计算即可,所以$| x | = \sqrt{a^{2}+b^{2}}$。
复数的乘法(假设为 $(a+bi) * (c+di)$ ) ,那么计算过程:
$(a+bi) * (c+di)$
$ = a(c+di) + bi(c+di)$
$ = ac+adi+bic+bidi$
$ = ac+adi+bi*c+bdi^{2}$
$ = ac+adi+bi*c-bd$
$ = (ac-bd) + (ad+bc)i$
共轭复数:
对于一个复数$c = a+bi$,其共轭复数表示为 $\bar c$。$\bar c = a - bi$,即,将复数部分取反。
$c * \bar c$
$=(a+bi) * (a - bi)$
$=a(a-bi) + bi(a-bi)$
$=a^{2}-abi + abi - b^{2}i^{2}$
$=a^{2}-abi + abi+b^{2}$
$=a^{2}+b^{2}$
可以发现,这就是 $c$的模长的平方。而模长为1时,$a^{2} + b^{2} = |c|^{2} = 1$(说废话呢)
单位根
设一个数 $x$ ,$x^{n} = 1$,那么 $x$就是一个 $n$ 次单位根。
将一个半径为$1$的圆分成n份,n个点分别就是一个 $n$次单位根。
看一下这张图:
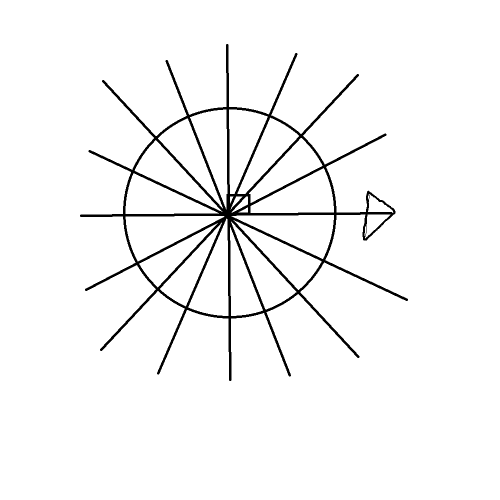
从箭头开始的那一点开始,逆时针将 $n$ 个 $n$ 次单位根编号,分别为$\omega^{1}{n},\omega^{2}{n}......\omega^{n}{n}$
$\omega^{k}{n} = cos(\frac{k}{n} \cdot 2\pi) + sin(\frac{k}{n} \cdot 2\pi)$。
${\omega^{1}{n}}^k = \omega^k_n$
$\omega^{k+\frac{n}{2}}_n = -\omega^{k}{n}$
推式子:
设多项式 $A(x) = \Sigma^{n-1}{0} a_i = a_0 + a_1x + a_2x^2 + a_3x^3 + ...... + a{n-1}x^{n-1}$
拆开,变成:
$(a_0 + a_2x^2 + a_4x^4 + ... + a_{n-2}x^{n-2}) + (a_1x + a_3x^3 + a_5x^5+ a_{n-1}x^{n-1})$
$= (a_0 + a_2x^2 + a_4x^4 + ... + a_{n-2}x^{n-2}) + x(a_1 + a_3x^2 + a_5x^4+ a_{n-1}x^{n-2})$
两边很相似。
设 $A1(x) = a_0 + a_2x^2 + a_4x^4 + ... + a_{n-2}x^{\frac{n}{2}-1}$
$A2(x) = a_1 + a_3x^2 + a_5x^4+ a_{n-1}x^{\frac{n}{2}-1}$
显然,$A(x) = A1(x^2) + x \cdot A2(x^2)$
设一个值 $k (k < \frac{n}{2})$,代入 $A(x)$:
$A(\omega^k_n) = A1({\omega^k_n}^2) + \omega^k_n \cdot A2({\omega^k_n}^2)$
$= A1({\omega^{2k}_n}) + \omega^k_n \cdot A2({\omega^{2k}_n})$
对于代入 $\omega^{\frac{n}{2} + k}_n$:
$A(\omega^{\frac{n}{2} + k}_n) = A1(\omega^{n+2k}_n) + \omega^{\frac{n}{2} + k}_n \cdot A2(\omega^{n+2k}_n)$
$= A1(\omega^{2k}_n \cdot \omega^n_n) - \omega^k_n \cdot A2(\omega^{2k}_n \cdot \omega^n_n)$
可以发现,$A(\omega^k_n)$ 和 $A(\omega^{\frac{n}{2} + k}_n)$ 结果仅仅是后半部分符号取反。
所以可以通过求前半部分直接得到后半部分。
FFT实现:
递归版 FFT 跑得慢,所以不使用递归版。
每个数的最终位置就是当前位置二进制反转之后的位置,所以可以提前改变位置。
代码(P1919):
#include <bits\/stdc++.h>
#include <complex>
using namespace std;
#define reg register
const double PI=acos(-1);
const int maxn=5e6+5;
typedef long long ll;
complex<double> a[maxn];
complex<double> b[maxn];
ll c[maxn];\/\/存储结果
int rev[maxn];
char given_a[maxn];
char given_b[maxn];
void FFT(complex<double>* num,int n,int inv)
{
for(reg int i=0;i<n;i++)
{
if(i<rev[i])
{
swap(num[i],num[rev[i]]);
}
\/\/提前更改为fft之后的序列
}
for(reg int mid=1;mid<n;mid<<=1)
{\/\/要处理序列大小的一半
complex<double> dwg(cos(PI\/mid),inv*sin(PI\/mid));\/\/单位根
for(reg int i=0;i<n;i+=(mid<<1))
{\/\/处理到的地方
complex<double> omega(1,0);
\/\/逐步求出omega(n,k)
for(reg int j=0;j<mid;j++,omega*=dwg)
{
complex<double> n1=num[i+j];
complex<double> n2=num[i+j+mid]*omega;
\/\/根据左边求出右边
num[i+j]=n1+n2;
num[i+j+mid]=n1-n2;
}
}
}
}
int main()
{
scanf("%s",given_a);
scanf("%s",given_b);
int len1=strlen(given_a);
int len2=strlen(given_b);
for(reg int i=0;i<len1;i++)
{
a[i]=given_a[len1-i-1]^48;
}
for(reg int i=0;i<len2;i++)
{
b[i]=given_b[len2-i-1]^48;
}
\/\/-------------------------
int newlen=1;\/\/计算结果位数
int bit_cnt=0;\/\/len1+len2二进制
while(newlen<=len1+len2)
{
newlen<<=1;
\/\/可以看作将其设为2的整数次幂
\/\/因为fft只能处理2的整数次幂
bit_cnt++;
}
for(reg int i=0;i<newlen;i++)
{
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit_cnt-1));
}
\/\/---------------------------------
FFT(a,newlen,1);
FFT(b,newlen,1);
for(reg int i=0;i<=newlen;i++)
{
a[i]*=b[i];
}
FFT(a,newlen,-1);
for(reg int i=0;i<len1+len2;i++)
{
c[i]=a[i].real()\/newlen+0.5;
}
for(reg int i=0;i<len1+len2;i++)
{
c[i+1]+=c[i]\/10;
c[i]%=10;
}
newlen=len1+len2+1;\/\/fft完成后,设置回原来的
while(c[newlen])\/\/处理剩余的仅为
{
c[newlen+1]+=c[newlen]\/10;
c[newlen]%=10;
newlen++;
}
while(!c[newlen])\/\/处理剩余的仅为
{
newlen--;
}
for(reg int i=newlen;i>=0;i--)
{
printf("%d",c[i]);
}
#ifndef ONLINE_JUDGE
system("pause");
#endif
return 0;
}

 鲁ICP备2025150228号
鲁ICP备2025150228号