本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-07-23 10:52:11

UPD：已修正格式错误。

题外话：

写一篇题解纪念第一次于 Div.2 切 D。

题意

给你一个 $n$ 行，$m$ 列的网格，每一列底部都有 $a_i$ 个障碍。
有 $q$ 次询问，每次询问给定一个起始坐标 $(x_s,y_s)$，一个终点坐标 $(x_f,y_f)$，以及一个正整数 $k$。
注意这里的 $x$ 代表第几行，$y$ 代表第几列。
你可以向前，向后，向左或向右走，但是每次都必须走 $k$ 步，并且不能走出网格或通过障碍。
问能否从起点走到终点。

$1 \le n \le 10^9$
$1 \le m \le 2 \cdot 10^5$
$1 \le q \le 2 \cdot 10^5$
$1 \le k \le 10^9$
保证给出的起点，终点不会在网格以外。

做法

来画一张图：

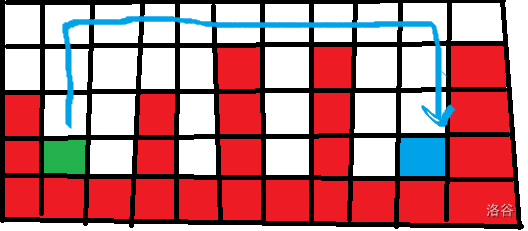
红色的障碍，绿色是起点，蓝色是终点。

显然，如果到达不了，怎么绕圈子都没有用。

先考虑一般的步骤，就是先向上走，避开障碍（到达一个没有障碍存在的行），然后向右走，走到终点所在的列，然后向下走到终点。

但是现在必须走 $k$ 步，所以有可能无法从起点到达没有障碍的那一行。
为了尽可能避开障碍，应该贪心的走到能走到的最高的，且不会越界的行。
显然这一行的行数就是 $(n-x_s) \bmod k$。
设 $maxh$ 代表起始列到终点列（$y_s$ 到 $y_f$）中最高的障碍的高度。
若 $(n-x_s) \bmod k \ge n - maxh$，那么说明无论如何都无法到达没有障碍的那一行，也就无法避开障碍到达终点的那一列，所以无解。
下一步就是判断从起点列能否通过走 $k$ 的倍数步到达 终点列，显然，如果 $\lvert y_f-y_s \rvert$ 不是 $k$ 的倍数，那么一定走不到。
最后，如果起始点与终点的高度差不是 $k$ 的倍数，那么仍然无解。

注：区间最高障碍可以用 st 算法求。

Code

#include <bits\/stdc++.h>
using namespace std;
namespace Main
{
    const int maxn=2e5+5;
    int n,m;
    int a[maxn];
    int q;
    int st[19][maxn];
    int log[maxn];
    void main()
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
        {
            scanf("%d",&a[i]);
        }
        for(int i=1;i<=m;i++)
        {
            st[0][i]=a[i];
        }
        for(int i=2;i<=m;i++)
        {
            log[i]=log[i>>1]+1;
        }
        for(int i=1;i<=18;i++)
        {
            for(int j=1;j<=m-(1<<i)+1;j++)
            {
                st[i][j]=max(st[i-1][j],st[i-1][j+(1<<(i-1))]);
            }
        }
        scanf("%d",&q);
        while(q--)
        {
            int x1,x2,y1,y2,k;
            scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&k);
            if(y2<y1)swap(y2,y1);
            int lo2=log[y2-y1+1];
            int imax=max(st[lo2][y1],st[lo2][y2-(1<<lo2)+1]);
            \/\/起始列到终点列最高障碍
            int sy=n-imax;\/\/最高障碍离顶部有多少行
            bool flag=1;
            int sy2=(n-x1)%k;\/\/最高能到达第几行
            if(sy2>=sy)
            {\/\/第一步判断
                flag=0;
            }
            if(abs(y2-y1)%k!=0)
            {\/\/第二步判断
                flag=0;
            }
            if(abs(x2-x1)%k!=0)
            {\/\/第三步判断
                flag=0;
            }
            if(flag)printf("YES\n");
            else printf("NO\n");
        }
    }
}
int main()
{
    Main::main();
    return 0;
}