题目背景

本题中合法括号串的定义如下：

1. () 是合法括号串。
2. 如果 A 是合法括号串，则 (A) 是合法括号串。
3. 如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

1. 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 $l$ 与终止位置 $r$ 来表示，记为 $S (l, r)$（$1 \leq l \leq r \leq |S |$，$|S |$ 表示 S 的长度）。
2. S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 $l$ 不同或 $r$ 不同。

题目描述

一个大小为 $n$ 的树包含 $n$ 个结点和 $n - 1$ 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 $n$ 的树，树上结点从 $1 \sim n$ 编号，$1$ 号结点为树的根。除 $1$ 号结点外，每个结点有一个父亲结点，$u$（$2 \leq u \leq n$）号结点的父亲为 $f_u$（$1 ≤ f_u < u$）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 $s_i$ 为：将根结点到 $i$ 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 $s_i$ 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 $i$（$1\leq i\leq n$）求出，$s_i$ 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 $s_i$ 共有 $k_i$ 个不同子串是合法括号串， 你只需要告诉小 Q 所有 $i \times k_i$ 的异或和，即：

$$ (1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) $$

其中 $xor$ 是位异或运算。

输入格式

第一行一个整数 $n$，表示树的大小。

第二行一个长为 $n$ 的由( 与) 组成的括号串，第 $i$ 个括号表示 $i$ 号结点上的括号。

第三行包含 $n − 1$ 个整数，第 $i$（$1 \leq i \lt n$）个整数表示 $i + 1$ 号结点的父亲编号 $f_{i+1}$。

输出格式

仅一行一个整数表示答案。

输入输出样例 #1

5
(()()
1 1 2 2

6

说明/提示

【样例解释1】

树的形态如下图：

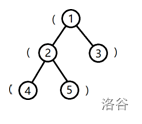
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 $0$。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 $0$。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 $1$。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 $0$。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 $1$。

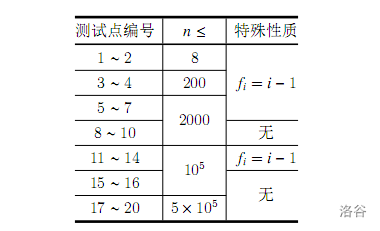
【数据范围】