题目背景

We could have had it all. . . . . .

我们本该，拥有一切

Counting on a tree. . . . . .

何至于此，数数树上

Counting on a Tree（CoaT）即是本题的英文名称。

题目描述

Access Globe 最近正在玩一款战略游戏。在游戏中，他操控的角色是一名 C 国士兵。他的任务就是服从指挥官的指令参加战斗，并在战斗中取胜。

C 国即将向 D 国发动一场秘密袭击。作战计划是这样的：选择 D 国的 $s$ 个城市，派出 C 国战绩最高的 $s$ 个士兵分别秘密潜入这 些城市。每个城市都有一个危险程度 $d_i$。

C 国指挥官会派遣战绩最高的士兵潜入所选择的城市中危险程度最高的城市，派遣战绩第二高的士兵潜入所选择的城市中危险程度次高的城市，以此类推（即派遣战绩第 $i$ 高的士兵潜入所选择城市中危险程度第 $i$ 高的城市）。D 国有 $n$ 个城市，$n - 1$ 条双向道 路连接着这些城市，使得这些城市两两之间都可以互相到达。为了任务执行顺利，C 国选出的 $s$ 个城市中，任意两个所选的城市，都 可以不经过未被选择的城市互相到达。

Access Globe 操控的士兵的战绩是第 $k$ 高，他希望能估计出最终自己潜入的城市的危险程度。Access Globe 假设 C 国是以等概率选出任意满足条件的城市集合 $S$，他希望你帮他求出所有可能的城市集合中，Access Globe 操控的士兵潜入城市的危险程度之和。如果 选择的城市不足 $k$ 个，那么Access Globe 不会被派出，这种情况下危险程度为 $0$。

当然，你并不想帮他解决这个问题，你也不打算告诉他这个值除以 $998\,244\,353$ 的余数，你只打算告诉他这个值除以 $64\,123$ 的余数。

输入格式

第 $1$ 行包含 $3$ 个整数 $n,k,W$，表示 D 国城市的个数，Access Globe 所操控士兵潜入的城市战绩排名以及 D 国的所有城市中最 大的危险程度；

第 $2$ 行包含 $n$ 个 $1$ 到 $W$ 之间的整数 $d_1, d_2, \ldots, d_n$，表示每个城市的危险程度；

第 $3$ 行到第 $n + 1$ 行，每行两个整数 $x_i, y_i$，表示 D 国存在一条连接城市 $x_i$ 和城市 $y_i$ 的双向道路。

输出格式

输出一个整数，表示所有可行的城市集合中，Access Globe 操控的士兵潜入城市的危险程度之和除以 $64\,123$ 的余数。

输入输出样例 #1

5 3 3
2 1 1 2 3
1 2
2 3
1 4
1 5

11

输入输出样例 #2

10 2 3
2 1 1 3 1 2 3 3 1 3
1 2
2 3
2 4
2 5
2 6
5 7
1 8
8 9
1 10

435

说明/提示

D 国地图如下，其中危险程度为 $d$ 的城市的形状是 $d + 3$ 边形。

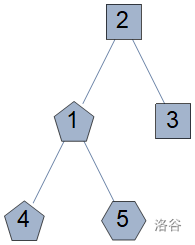
以下是所有符合条件且选择的城市不少于 $3$ 个的方案：

• 选择城市 $1,2,3$，Access Globe 的士兵潜入的城市危险程度为 $1$；
• 选择城市 $1,2,3,4$，Access Globe 的士兵潜入的城市危险程度为 $1$；
• 选择城市 $1,2,3,5$，Access Globe 的士兵潜入的城市危险程度为 $1$；
• 选择城市 $1,2,3,4,5$，Access Globe 的士兵潜入的城市危险程度为 $2$；
• 选择城市 $1,2,4$，Access Globe 的士兵潜入的城市危险程度为 $1$；
• 选择城市 $1,2,5$，Access Globe 的士兵潜入的城市危险程度为 $1$；
• 选择城市 $1,2,4,5$，Access Globe 的士兵潜入的城市危险程度为 $2$；
• 选择城市 $1,4,5$，Access Globe 的士兵潜入的城市危险程度为 $2$；
• 而在选择的城市少于 $3$ 时，Access Globe 的士兵潜入的城市危险程度均为 $0$。

所以你应该输出 $(1 + 1 + 1 + 2 + 1 + 1 + 2 + 2) \bmod 64\,123 = 11$。

\begin{array}{|c|c|c|c|c|} \hline \textbf{测试点} & n= & k\leq & W= & \textbf{地图是一条链} \\ \hline 1 & 3 & n & 1,666 & \textbf{保证} \\ \hline 2 & 15 & n & 1,666 & \textbf{不保证} \\ \hline 3 & 20 & n & 1,666 & \textbf{不保证} \\ \hline 4 & 300 & n & 10 & \textbf{保证} \\ \hline 5 & 1,666 & n & 1,666 & \textbf{保证} \\ \hline 6 & 50 & n & 1,666 & \textbf{不保证} \\ \hline 7 & 200 & n & 1,666 & \textbf{不保证} \\ \hline 8 & 500 & n & 1,666 & \textbf{不保证} \\ \hline 9 & 1,111 & 10^2 & 10^2 & \textbf{不保证} \\ \hline 10 & 1,111 & 50 & 1,111 & \textbf{不保证} \\ \hline 11 & 1,111 & 10^2 & 1,666 & \textbf{不保证} \\ \hline 12 & 1,666 & 10^2 & 1,666 & \textbf{不保证} \\ \hline 13 & 1,666 & 200 & 1,666 & \textbf{不保证} \\ \hline 14 & 1,666 & 500 & 1,666 & \textbf{不保证} \\ \hline 15 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline 16 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline 17 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline 18 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline 19 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline 20 & 1,666 & n & 1,666 & \textbf{不保证} \\ \hline \end{array}