题目描述

小 T 正在研究某段时间中所发生的事件。经观测，有 $n$ 个编号为 $1\sim n$ 的事件在这段时间内按顺序依次发生，第 $i$ 个发生的是事件 $p_i$。这个描述事件发生顺序的排列 $p$ 可称为这段时间的时间线。

突然，邪恶生物小 S 攻击了这条时间线，将这 $n$ 个事件的发生顺序 $p$ 变为了在所有长为 $n$ 的排列中等概率随机选取的一个排列。不仅如此，小 S 还用剪刀把时间线剪断，通过进行 $k$ 次操作，将排列 $p$ 分割成了 $(k + 1)$ 段。

具体而言，在小 S 进行第 $i$ 次操作时，排列 $p$ 和之前所有插入的剪断点构成了一个长度为 $(n + i - 1)$ 的序列。该序列包括所有相邻元素之间和序列开头、末尾处共有 $(n + i)$ 个插入位置。小 S 将从这些插入位置中等概率随机选取一个位置，插入一个新的剪断点。最后，小 S 从最终被插入的 $k$ 个剪断点处把序列剪开，将排列 $p$ 分割成了 $(k + 1)$ 段序列。这 $(k + 1)$ 段序列中可能有空序列。

为了拯救这条即将毁灭的时间线，小 T 决定把这 $(k + 1)$ 段序列按某种顺序重新拼接成一个长度为 $n$ 的排列，形成一条新的时间线。不过，由于事件之间存在一定的逻辑关系，事件的发生时间之间也存在一些先后顺序要求。经研究，共存在 $m$ 条先后顺序要求 $(u, v)$，要求事件 $u$ 的发生时间必须在事件 $v$ 之前。也就是说，$u$ 在时间线中的出现位置必须在 $v$ 之前。

请你设计程序，计算有多大的概率，存在至少一种重新排列这 $(k + 1)$ 段序列，并将其重新拼接为一条新的时间线的方案，能够使所有的 $m$ 条事件发生时间之间的先后顺序要求都得到满足。

为了避免精度误差，请你输出答案对 $10^9 +7$ 取模的结果。形式化地，可以证明答案可被表示为一最简分数 $\frac{p}{q}$，请你输出一个 $x$ 满足 $0 \le x < 10^9+7$ 且 $qx \equiv p \pmod {10^9+7}$。可以证明在题目条件下这样的 $x$ 总是存在。

输入格式

第一行三个整数 $n, m, k$，分别描述事件的个数，事件之间先后顺序的条数以及小 S 进行的剪断操作次数。

接下来 $m$ 行，每行两个整数 $u, v$，表示一条事件发生时间的先后顺序要求。

输出格式

输出一行一个整数，表示所求答案。

输入输出样例 #1

2 1 1
1 2

666666672

输入输出样例 #2

3 0 2

1

输入输出样例 #3

4 4 4
1 2
1 3
1 4
2 4

937500007

说明/提示

【样例 1 解释】

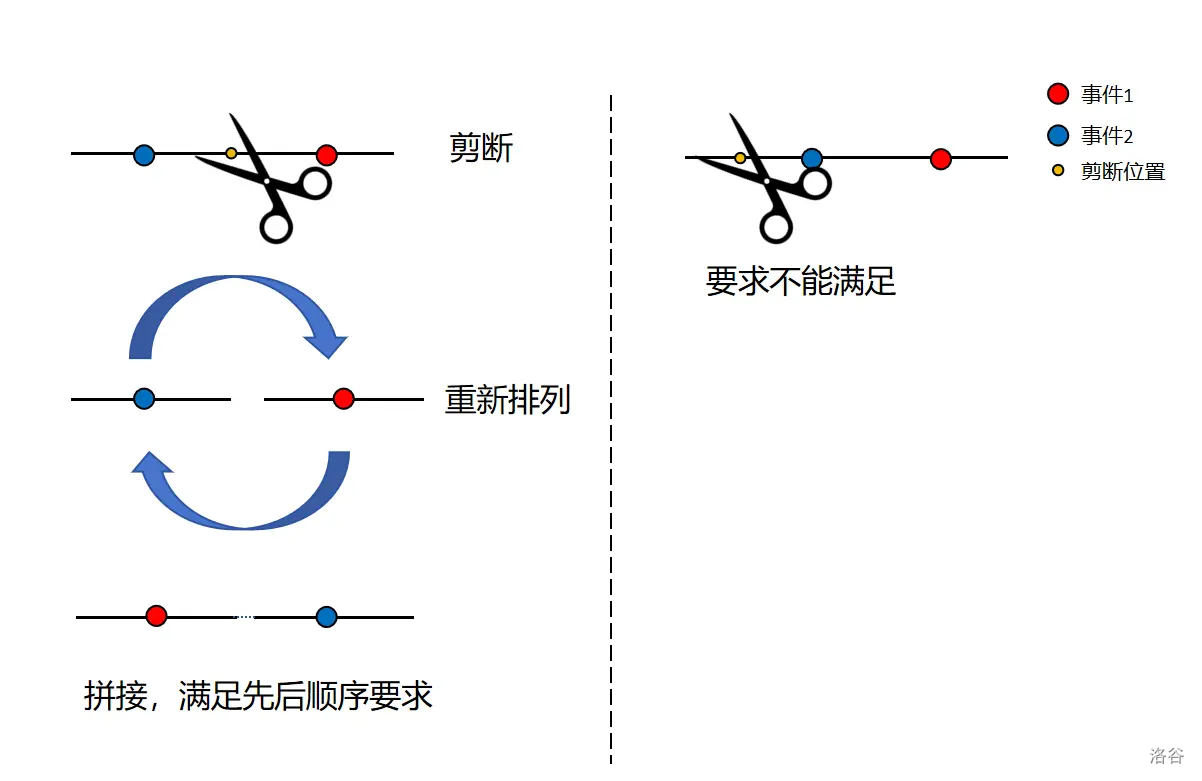
假如事件 $1$ 的发生时间早于事件 $2$，那么无论怎样拼接都是可行方案，一定可以满足要求。否则，只有剪断时间线的位置位于事件 $1$ 和事件 $2$ 的发生时间之间，才能满足要求。答案为 $\frac{1}{2}+\frac{1}{2}\times \frac{1}{3}=\frac{2}{3}$。

【样例 2 解释】

没有任何事件发生时间之间的先后顺序要求，因此无论怎样拼接都是可行的方案，答案为 $1$。

【样例 4】

见附件中的 timeline4.in/ans。

【样例 5】

见附件中的 timeline5.in/ans。

该组样例满足数据范围中的特殊性质 B。

【样例 6】

见附件中的 timeline6.in/ans。

该组样例满足数据范围中的特殊性质 A。

【样例 7】

见附件中的 timeline7.in/ans。

【子任务】

对于所有测试数据，

• $1 \le n \le 15$，
• $0 \le m \le \frac{n(n-1)}{2}$，$0 \le k \le n$，
• $1 \le u < v \le n$，保证不存在两对 $(u,v)$ 完全相同。

\begin{array}{|c|c|c|c|c|} \hline \textbf{测试点} & n & m & k & \textbf{特殊性质} \\ \hline 1 & \le 3 & =n-1 & =0 & B \\ \hline 2 & \le 5 & \le \frac{n(n-1)}{2} & \le n & \textbf{无} \\ \hline 3,4 & \le 14 & =n-1 & \le n & B \\ \hline 5 & \le 14 & =n-1 & =0 & A \\ \hline 6 & \le 14 & =n-1 & \le n & A \\ \hline 7 & \le 14 & =0 & \le n & \textbf{无} \\ \hline 8 & \le 14 & =\frac{n(n-1)}{2} & \le n & \textbf{无} \\ \hline 9,10 & \le 9 & \le 15 & \le n & \textbf{无} \\ \hline 11 & \le 13 & \le \frac{n(n-1)}{2} & =0 & \textbf{无} \\ \hline 12 & \le 13 & \le \frac{n(n-1)}{2} & \le n & \textbf{无} \\ \hline 13 \sim 17 & \le 14 & \le \frac{n(n-1)}{2} & \le n & \textbf{无} \\ \hline 18\sim 20 & \le 15 & \le \frac{n(n-1)}{2} & \le n & \textbf{无} \\ \hline \end{array}

特殊性质 A：对于每个事件 $x$，至多存在一条先后顺序 $(u, v)$ 使得 $v = x$。

特殊性质 B：对于所有先后顺序 $(u, v)$，均满足 $u = 1$。