本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-11-19 01:13:47

输麻了，G 的正确代码差 1s 交上，F 干脆没做。
总之手速还是不行。Div.3 没啥难题， AK 难度就在于手速。

A

如果第一次 Vanya 没赢，那么 Vova 就可以重置，让他永远不赢。

B

参考 $n$ 的最大因子个数。
暴力能过。

C

设 $dp_i$ 表示右端点为 $i$ 的最大大小。

若 $a_i$ 和 $a_{i-1}$ 奇偶不同，$dp_i = \max(a_i,dp_{i-1}+a_i)$
否则，$dp_i = a_i$

最后答案是 $\max(dp_1,dp_2,\cdots,dp_n)$

D

设 $pw_i$ 为 $a_i$ 的质因数分解中 $2$ 的出现次数。
设 $bs_i$ 为 $\frac{a_i}{2^{pw_i}}$。

由小学数学可以推导得知，$i,j$ 能配对，当且仅当 $pw_i - a_i = pw_j - a_j$。

然后 map 统计一下就好了。

E

最终要求没有任意一个 $i$ 使得 $a_i \gt a_{i+1}$。

考虑每次操作的影响。

如果 $a_i \gt a_{i+1}$，那么它本质上消除了一对不合法的数对。

否则相当于不改变。

依次操作下来，当最后一个不合法的 $i$ 被执行操作，排序也就完成了。
设最后一个不合法的 $i$ 为 $lst$。

考虑 $[1,lst]$ 之间每个 $i$ 被执行的影响。

第 $i$ 个，如果跳出了 $[1,lst]$ 的范围，那么没啥事。
如果没跳出（只要是没跳到 $lst$ 后面就算），那么稍稍想一下依赖关系，必然是陷入了无限循环，无解。

那么如何判断无限循环呢？

只要有 $[1,lst]$ 任意一个 $i$ 操作之后位置不改变，那么一定陷入无限循环，从而间接导致其他的 $i$ 跳不出去。

F

默认根是 $1$。

为了方便实现，我们可以仅仅用两条链构造出两个距离为 $d_i$ 的叶子。

先根据 $d_1$ 构造出大概是这样的两条链（从 $1$ 出发）：

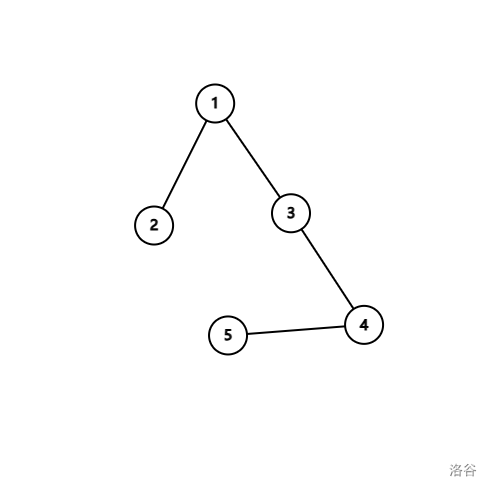
第一条链长度固定是 $1$，而第二条链的长度则根据 $d_i$ 进行变化，这个例子中，$d_i = 4$。

剩下的节点干什么呢？因为第二天链的长度需要时刻变化，所以我们还是从 $1$ 出发，新建第三条链，进行存储。

大概长这样（$n=8,d_i=4$)

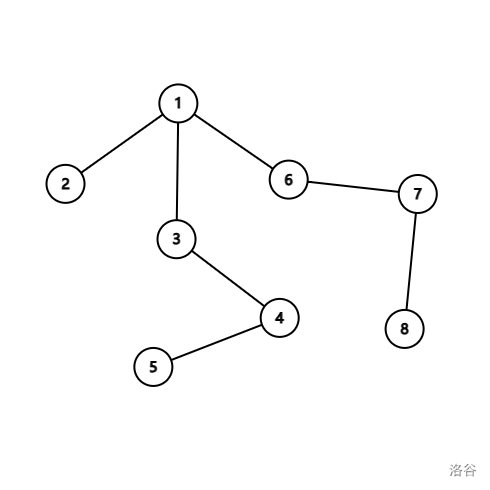
第 $3$ 条链是 $1,6,7,8$ 组成的。

需要适应 $d_i$ 时，直接配合第三条链进行切割/接尾操作就行。

我为了方便开了 $3$ 个 std::list

G

我们可以将这个问题转化为一个更清新的问题：

给定一个数列 $p$，并推导得到一个数列 $p{'}$。

设 $size_i$ 为 $i$ 为根的子树大小，$dfn_i$ 是 $i$ 的 dfs 序。

$p{'}_i$ 是节点 $p_i$ 的 dfs 序。

每次询问给定 $l,r,x$，求是否存在 $i$，使得 $l \le i \le r$，且 $dfn_x \le p'_i \le dfn_x + size_x - 1$。

这种操作，log 数据结构似乎不大好做，自然联想到优雅的暴力——分块。
具体的，每个块预处理哪些 $p'$ 值出现过，并开桶记录（由于任意 $p'_i$ 不会超过 $n$，所以可以用桶）

接下来每个块就可以 $O(1)$ 判断某个值域区间是否有数存在了。

预处理复杂度 $O(n \sqrt n)$，查询复杂度 $O(q \sqrt n)$。