本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2021-12-05 15:03:18

我们来看一个图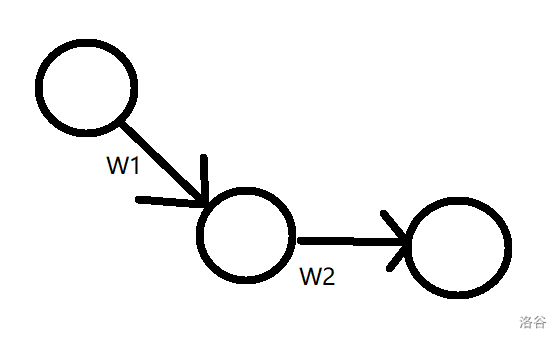： 从最上边的点，到最后一个点，边权是： $(w_1 + w_2)^2$

那么从一个点到另一个点，需要两步：

• 第一步，移到中间点。
• 第二步，移到目标点。

我们把点分为两类：

• 1. 到达点：到达点就是到达一个点的最短路是多少
• 2. 中转点：中转点就是要到达一个地方经过的点

如果我们把路径分为两种：

一： 中转点 $\impliedby$ 到达点，花费0边权

二： 到达点 $\impliedby$ 中转点，花费 $(w_1 + w_2) ^ 2$

但如果这样做的话，复杂度会很高，中转点的状态数是 $n^2$

但当前我们只关注 $w_1$ 是谁，而不关注中转点是谁。

所以我们可以把中转点改一下，中转点的状态数只有 $[50]$ 个就够了，因为 $w_i$ 最多只有 50。

$u_0$ 代表到达点 ， $u_1$ 代表u是中转点，他是由1走过来的。

这就维护了他的最短路 $dis_{[u][0]} ,dis_{[u][1]} ……. dis_{[u][50]}$ 。

他的时间复杂度为 $\mathcal{O(n·mlongm)}$

看代码：

#include <bits\/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;\/\/根据题目范围
#define ll long long
#define itn int \/\/个人习惯，防手残
vector< pair<int , int> > e[maxn];\/\/定义变量
int n , m;
ll dis[maxn][55];
inline void dij() {
	memset (dis , 0x3f , sizeof (dis));\/\/每次用的时候，要初始化
	dis[1][0] = 0;
	priority_queue< pair <ll , pair<int , int> > > pq;
	pq.push({0 , {1 , 0}});
	while (!pq.empty()) {
		auto now = pq.top(); pq.pop();
		int u = now.second.first , u2 = now.second.second;
		for (auto &x : e[u]) {
			int v = x.first , w = x.second;
			if (u2 > 0) {
				if (dis[v][0] > dis[u][u2] + (u2 + w) * (u2 + w)) {
					dis[v][0] = dis[u][u2] + (u2 + w) * (u2 + w);
					pq.push({-dis[v][0] , {v , 0}});
				}
			}else {
				if (dis[v][w] > dis[u][u2]) {
					dis[v][w] = dis[u][u2];
					pq.push({-dis[v][w] , {v , w}});
				}
			}
		}
	}
}
int main() {
	cin >> n >> m;\/\/读入
	for (int i = 0; i < m; ++ i) {\/\/读入边
		int u , v , w;
		cin >> u >> v >> w;
		e[u].push_back({v , w});
		e[v].push_back({u , w});
	}
	dij();\/\/调用函数
	for (itn i = 1; i <= n; ++ i)\/\/输出
		if (dis[i][0] > int(1e18))cout << "-1 ";
		else cout << dis[i][0] << ' ';
	return 0;
}