本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2022-05-01 20:08:34

题解思路：

图就是一个内接圆，外面有一圈外接圆。

外接圆有 $n$ 个。

我们就设内接圆的半径为 $r$ 外接圆的半径为 $R$

如下图所示：

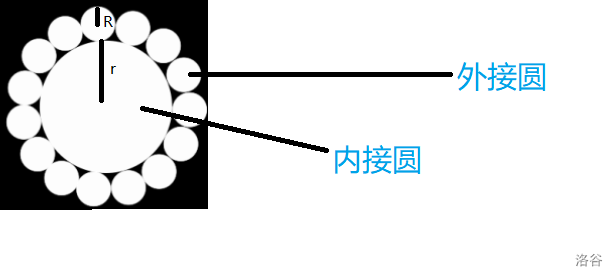
然后我们随便挑两个圆来看，首先我们先把圆心连起来，因为这 $n$ 个圆是相等的，所以他是等腰三角形，用两个外接圆的重合的那个点和内接圆的圆心连起来就是和外接圆的圆心连起来的边是垂直的，如下图所示：

而在圆心里的哪个角我们能求出来，因为 $n$ 个这样的角组成了一个圆，所以他的角度为：$\frac{2\pi}{n}$。

如图：

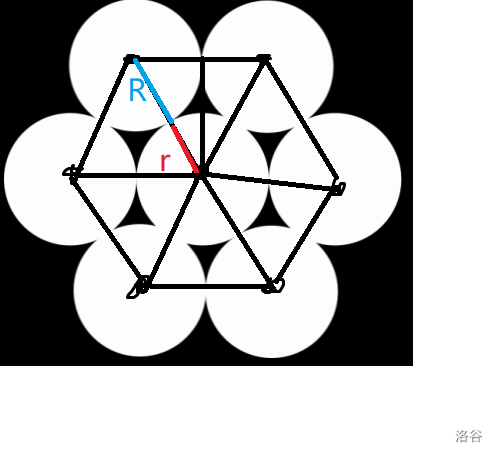
那么这个角的一半就是： $\frac{\pi}{n}$。

那么 $\frac{R}{R + r} = \sin \frac{\pi}{n} \longrightarrow R = \frac{r \sin\frac{\pi}{n}}{1 - \sin \frac{\pi}{n}}$。

公式好了，就可以写代码了！

AC CODE:

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const double PI = 3.1415926;
double n , r;
int main() {
    cin >> n >> r;
    printf ("%.7lf\n" , (double)(r * sin (PI \/ n)) \/ (1.0 - sin (PI \/ n)));\/\/直接套用公式即可
    return 0;
}

码字不易，求赞！