本文章由 WyOJ Shojo 从洛谷专栏拉取,原发布时间为 2022-05-05 20:38:14
题解思路:
我们发现:
当搭高度为 $1$ 时,那么他就只用两个牌。
当塔高度为 $i$ 时,那么他就是把第 $i - 1$ 个封口在加上 $i$ 个尖,如图:
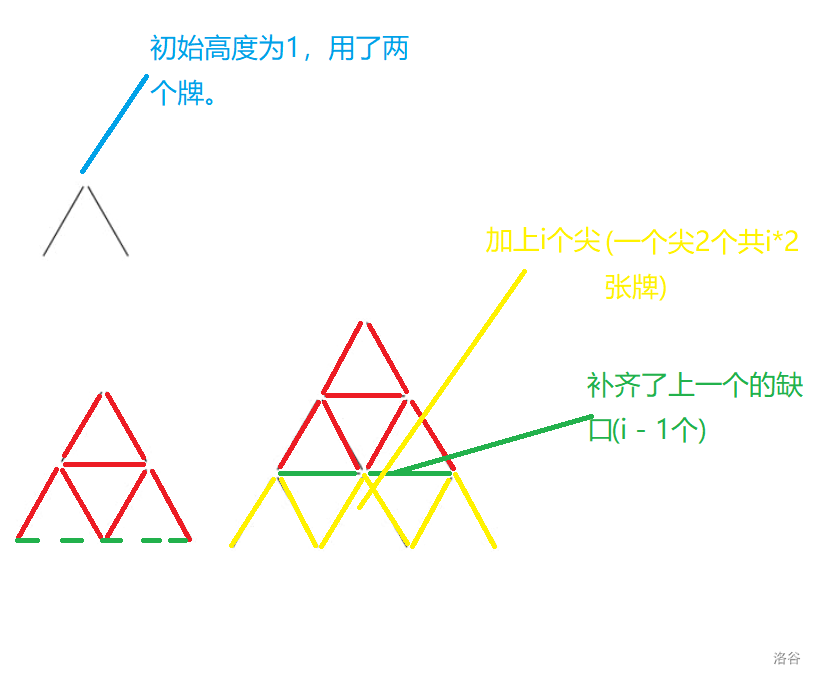
就的到了一下公式:($f_{i}$ 代表高为 $i$ 的金字塔的牌的数量)
$\left\{\begin{matrix} f_{1} = 2\ f_{i} = f_{i - 1} + i - 1 + 2 \times i \end{matrix}\right.$
然后根据题意二分求出第一个 $\le$ 牌数的 $f$ 值,然后减去就可以了!
AC CODE:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
int T;
int cnt;
int f[100010];
void init () {
f[1] = 2;
for (cnt = 2; f[cnt - 1] <= 1000000000; ++ cnt)
f[cnt] = f[cnt - 1] + cnt - 1 + 2 * cnt;\/\/预处理搭建i高的金字塔的纸牌数
}
int main() {
init ();
-- cnt;\/\/因为是第一个>1000000000的才会跳出,所以,cnt要--
scanf ("%d" , &T);
while (T --) {
int n;
scanf ("%d" , &n);
int ans = 0;
int mid = 0;
do {
int l = 1 , r = cnt;
while (l <= r) {\/\/二分
mid = (l + r) >> 1;
if (f[mid] == n) break;\/\/找到了直接退出
else if(f[mid] < n) l = mid + 1;
else r = mid - 1;
}
if (f[mid] > n) mid --;\/\/若比他大了就--
if (mid <= 0) break; \/\/若mid小于等于0就是没有小于等于n的了
n -= f[mid];\/\/减去用的纸牌数
ans ++;\/\/搭了一个
}while (true);
printf ("%d\n" , ans);
}
return 0;
}
码字不易,求赞!

 鲁ICP备2025150228号
鲁ICP备2025150228号