本文章由 WyOJ Shojo 从洛谷专栏拉取,原发布时间为 2024-06-17 06:14:55
这能绿?
由于 Alice 的路线不能往回走,所以他走的路线一定是这样的(红色是喷泉):
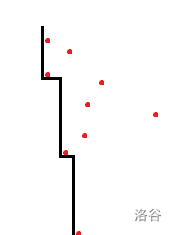
那么我们发现,只有移走拐点且最小值变小后才会增加。
那么我们考虑维护后缀 $\min$,然后对于 $x$ 相同的点,若哪一个 $y$ 会使当前 $\min$ 变小,那么移走这个点;若有多个 $y$ 会使 $\min$ 变小,那么取使 $\min$ 变小最多的那个 $y$。
然后这一段路程就是当前 $\min$ 乘这段路程的长度 $x_i-x_{i-1}(x_i \not= x_{i-1})$。
#include <bits\/stdc++.h>
using namespace std;
typedef long long ll;
int T;
int n, m, k;
array<int, 3> a[200010];
int is[200010];
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= k; ++i) scanf("%d%d", &a[i][0], &a[i][1]), a[i][2] = i;
sort(a + 1, a + 1 + k);
ll minn = m + 1;
ll sum = (minn - 1) * (n - a[k][0]);
for (int i = k; i >= 1; --i) {
int id = 0;
if (a[i][1] < minn) id = a[i][2];
minn = min(minn, 1ll * a[i][1]);
while (i - 1 >= 1 && a[i - 1][0] == a[i][0]) {
if (a[i - 1][1] < minn) id = a[i - 1][2];
minn = min(minn, 1ll * a[i - 1][1]);
--i;
}
sum += 1ll * (minn - 1) * (a[i][0] - a[i - 1][0]);
is[id] = true;
}
printf("%lld\n", sum);
for (int i = 1; i <= k; ++i) printf("%d ", (int)is[i]);
puts("");
for (int i = 1; i <= k; ++i) is[i] = 0;
}
return 0;
}

 鲁ICP备2025150228号
鲁ICP备2025150228号