本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-12 09:48:57

A:

思考的时候通过矩阵思考的。 题目翻译 给你一棵以 1为根的树，i 号点的父亲是 Pi，点权是 Ai，重复无限次，从 1∼N 分别将 i 号点的点权加进其父亲的点权。请判断1 号点点权的正负性。

推导： 设一个小的矩阵A,大小为$N*N$，变换$10^{10}$次，求变换后的矩阵$%P$

翻译题解：

如果我们遵循$P_j→P_i→⋯P_1$的顺序，我们最终会到达1。设i的深度$di$为从$i$到达1所需要的→个数。 对于每一个$j(0≤j<N)$，设$B_j$为$A_i$对所有i的和，使$d_i =j$。 首先，$a_1 = b_0$。 有一个运算可以表示为$ B_j+=$ $B_{j+1}$ $(0 \leq j < N)$。

如果所有的$b_j$都是0，那么不管我们操作多少次，$b_0$都是$0$，所以答案是$0$。

假设有一个不为零的$B_j$。现在，我们取最大的$j$使得$B_j !=0$，我们称它为$k$.

• 考虑$B_k >0$的情况。

首先，因为$B_j (j>k)$都是$0$，所以$B_k$的值是常数。

$\space \space$特别是，它总是正的。 接下来，考虑$B_{k-1} $。这个值随着每次操作增加$B_k$，所以即使初始值是负的，在足够数量的操作之后，它总是正的。接下来，考虑$B_{k-2}$。由前面的讨论可知，经过足够次数的运算后，$B_{k-1} $总是正的。因为这个$B_{k-1} $被加到$B_{k-2} $，最终$B_{k-2} $也会变成正数。重复这个论点，我们可以看到，在足够多的操作之后，即使$B_0$也会变成正数。

因此，在这种情况下，答案是$+$。

• 对于$B_k <0$的情况.可以类似地进行讨论，我们可以看到答案是$-$。

这里，我们使用了表达式“a enough number of times”，但是如果我们正确地计算，我们可以看到$10^{100}$是足够的。

它可以通过使用二项式系数计算每个$A_i$的贡献来完成，尽管细节被省略了。如果我们按照上面的判断执行，我们可以在$O(N)$时间内解决问题。

官方题解，以上翻译结果来自有道神经网络翻译（YNMT）·

在思考过程中，我们可以把矩阵变换写下来，发现变换的系数二项式定理的展开项。

随着系数的增大，后面的项权值变大，原始的ai值所占比重越来越小。可以推导出前面的转移关系。

\/*
1<=pi<i， api +=ai,
首先明确了这是一颗树，不存在环。而且都是下标小的数累加上下标大的数
因为是进行无限次变换。
那么树最底层的累加会依次向上传递。每个数都收到下一层的影响。因此从最底层开始判断
如果为0那决定不了影响
如果非零那就最后影响到A1为正，为负则A1为负。 
因为小的受大的影响，实际为一个拓扑。可以写dfs，也可以写逆序循环。

可以先写一个矩阵转移变换，建立一个实际印象。
转换时候的系数变换类似二项式定理。实际是矩阵的次方的形式。 
 
5
1 -1 1 -1 1
1 1 2 2
0 1 1 2 2 后移到一个。正好把需要处理的数加上。
A1+=A[2] A1+=A[3]
A[2]+=A4,A2+=A[5]
*\/
#include<bits\/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int MAXN = 2.5e5 + 5;

int a[MAXN], p[MAXN], dep[MAXN];
ll bak[MAXN];

int main(void)
{
	int n;
	scanf("%d",&n);
	for(int i=1; i<=n; ++i)
		scanf("%d",&a[i]);
	for(int i=2; i<=n; ++i)
		scanf("%d",&p[i]);
	
	for(int i=2; i<=n; ++i)
		dep[i] = dep[p[i]] + 1;
	
	for(int i=1; i<=n; ++i)\/\/每层的变换可以打包合并在一起。
		bak[dep[i]] += a[i];
	for(int i=n; i>=0; --i)
		if(bak[i] != 0)
		{
			if(bak[i] > 0)
				printf("+");
			else
				printf("-");
			return 0;
		}
	printf("0");
	return 0;
}

B

要计算单个区间的$f$，用贪心算法，从左端尽可能多地获取。

要计算所有区间的$f$，从每个左端点$l$开始。

对每个端点$i$,还要找出最右侧的$r$使得$\sum_{j=i}^{j<=r}a_j<S $

对于每一个 定义$dp[i]=\sum_{j=i}^N f(A[i,j])$。为方便起见，设$dp[N+1]=0$。

因此我们要倒着求$dp[i]$,$i=N,N-1,...1$

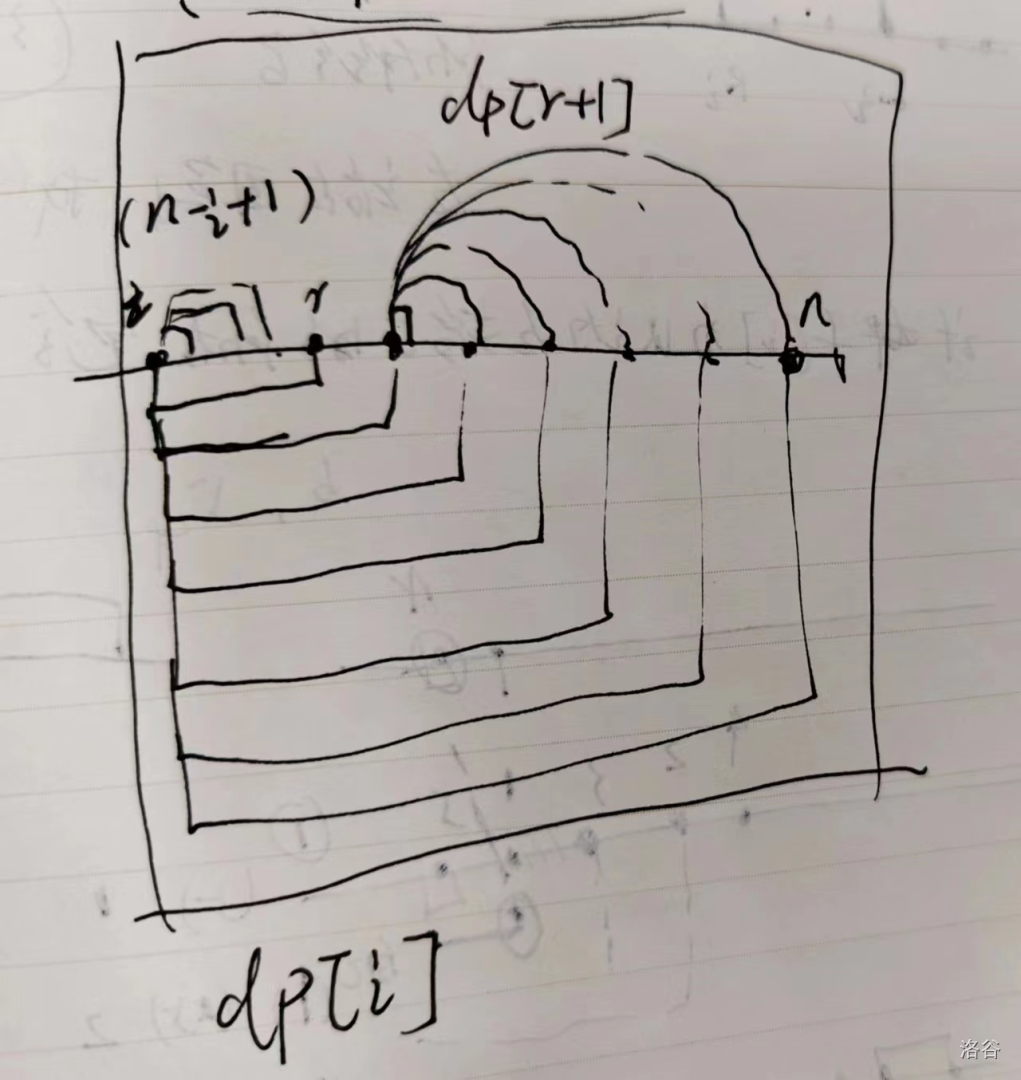
对于一个左端点$i$，设其右侧的端点r为划分到和$\leq S$的最右侧位置。$i,i+1,...,r,r+1,... n$

• 对于端点$j>=r$

  • 这一段作为整体贡献增加1，这样的数共有$n-r+1$个。
  • 这一段后面的贡献为 $dp[r+1]$

• 对于端点$j<r$ 从i开始到j使得贡献怎加1.这样的$j$共有$r-i$个.

因此，总的动态规划方程为 $dp[i]=dp[r+1]+N-r+1+r-i$

$dp[i]=dp[r+1]+N+1-i$

最终的答案是$\sum_{i=1}^{i<=n} dp[i]$

参考代码

\/*
考虑一段的贡献
l    r ,以l为左端点，这段和和<=s最右侧的位置为j
如果这段被计数，那么r+1到n都统计上了。
或者右端点不超过r的这段区间
f[l]=f[r]+(r-l)+n-l+1;

*\/
#include<bits\/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int MAXN = 2.5e5 + 5;

ll a[MAXN];
ll sum[MAXN], dp[MAXN];
int main(void)
{
	int n; ll S;
	scanf("%d%lld",&n,&S);
	for(int i=1; i<=n; ++i)
		scanf("%lld",&a[i]);
	

	for(int i=1; i<=n; ++i)
		sum[i] = sum[i-1] + a[i];
	
	ll ans = 0;
	for(int i=n; i>=1; --i)
	{
		int j = upper_bound(sum+i, sum+n+1, sum[i-1] + S) - sum;
		dp[i] = (j-i) + dp[j] + (n-j+1);
		ans += dp[i];
	}
	
	printf("%lld\n",ans);
	return 0;
}