本文章由 WyOJ Shojo 从洛谷专栏拉取,原发布时间为 2025-06-17 18:45:58
阅读方式:PDF(强烈推荐)
最大流、最小割、费用流
定义
网络(Network): 有向图 $G=(V,E)$,边 $(u,v)\in E$ 有容量 $c(u,v)$ 和流量 $f(u,v)$。通常来讲,存在两个特殊点:源点 $S$ 和汇点 $T$。如果边 $(u,v)$ 不存在,默认 $c(u,v)=0$。
可行流(Flow):从边集 $E$ 到整数集或实数集的函数,满足如下性质:
- 容量限制: $\forall (u,v)\in E$,$0\le f(u,v)\le c(u,v)$。每条边的流量不超过每条边的容量。
- 流量守恒: $\forall u\in V\setminus \set{S,T}$,$\sum_{(v,u)\in E} f(v,u)=\sum_{(u,v)\in E} f(u,v)$。除源点和汇点外,流入每个点的流量等于流出每个点的流量。
- 斜对称性: $\forall (u,v)\in E$,$f(u,v)=-f(u,v)$。从 $u\to v$ 流 $f(u,v)$ 的流量,等价于从 $v\to u$ 流 $-f(u,v)$ 的流量。

如图所示,网络可以想象成若干个过水装置,其中 $S$ 为出水装置,$T$ 为入水装置,边想象成管道,容量为管道最多承载的水,流量即为实际中的水流。那么,一张可行流就是与实际生活相符的流水的方式:容量限制——每个管道内的流量不能超过至多承载的水;流量守恒——除出水口和入水口外,其余点进去的必然要和出去的相同。
定义可行流的流量为 $s$ 点流出的流量之和或 $t$ 点流入的流量之和,即 $$ \sum_{(s,u)\in E} f(s,u)=\sum_{(u,t)\in E} f(u,t) $$ 相等的原因很简单,还是从出入水装置的角度考虑。因为从 $s$ 点流出的水最终流向 $t$ 点,中间又不会存水,所以必然是相等的。
残量网络(Residual Network):残量网络 $G_f=(V,E_f)$,其中 $E_f=\set{(u,v)\mid c_f(u,v)>0}$。$c_f(u,v)=c(u,v)-f(u,v)$。
⚠️注:由于上文所提到的斜对称性,$f(u,v)$ 存在负值,所以 $E_f$ 可能存在 $E$ 中的反向边。
割(cut): 把 $V$ 分成两个点集 $s\in S,t\in T$,$S\cup T=V$。则割的容量 $$ c(S,T)=\sum_{u\in S}\sum_{v\in T} c(u,v) $$ 最大流、最小割(maxflow, mincut): 最大流指最大的割的流量,最小割指最小的割的容量。
最小费用最大流(mincost, maxflow):费用流指每条边不仅有容量还有费用,最终的费用定义为每条边的费用 $\times$ 每条边的流量之和。
如何求解最大流、最小割便是本节所要讨论的问题,接下来探讨最大流和最小割之间的关系。
最大流最小割定理
若笔者记得没错,定理的内容本身是很长的,证明也较为复杂(好像有 $3$ 条来着)。为了贴合 OI,这里言简意赅地解释核心。
核心: 最大流等于最小割。
证明: 相信大家都不喜欢枯燥无味的数学证明,这里从直观上证明一下。
任意可行流的流量 $\le $ 该可行流的任意割的容量:因为从出入水装置的角度思考,割相当于将管道劈断,想象一下可行流在该横截面流过的水,必然不能超出所有劈断管道的容量之和,否则就盛不下了。
存在可行流,满足某个割等于该可行流的流量:该可行流需要满足残量网络上 $s$ 无法到达 $t$。选取在残量网络 $s$ 所能到达的所有点作为 $S$,则 $T=V\setminus S$。这样, $$ \forall u\in S,v\in T, c_f(u,v)=c(u,v)-f(u,v)=0 $$ 即,$f(u,v)=c(u,v)$。所以,$c(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)=可行流的流量$。
综上,可以得出最大流等于最小割。
Ford–Fulkerson 增广
有的读者可能问,为什么要定义残量网络?有的读者可能问,为什么要考虑 $-f(u,v)$ 的反向边?其实,这一切的一切,均是为了解决最大流问题。
直接的求解最大流的思路是每次在网络中找到一条还能流 $>0$ 的流量的路径(增广路径),并将流量增加上去。
很可惜,这是错的!如下图所示
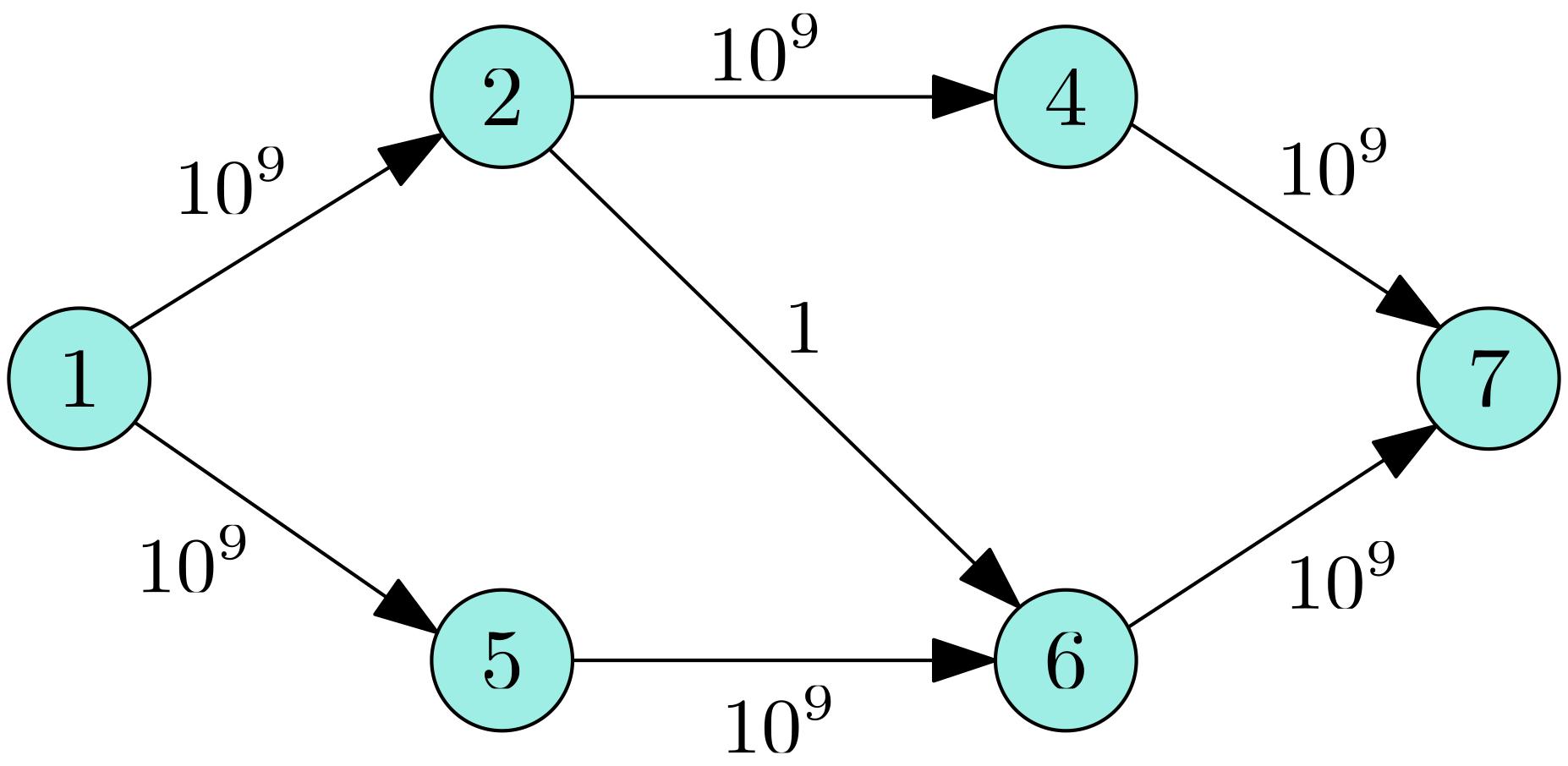
如果最初选择了 $1\to 2\to 6\to 7$ 这条增广路径,流量为 $1$,则接下来只能选择 $1\to 2\to 4\to 7$ 和 $1\to 5\to 6\to 7$ 这两条路径,均有 $10^9-1$ 的流量,总共 $2(10^9-1)+1=2\times 10^9-1$。而实际上最大流是只流 $1\to 2\to 4\to 7$ 和 $1\to 5\to 6\to 7$,能获得 $2\times 10^9$ 的流量。
所以,我们需要反悔!所以,这就是加入反向边的原因,流反向边等价于将之前流的退回去,这个操作称之为推流。
于是,我们得到了一个求解最大流的方法,每次找出一条增广路,对应更新边的流量和反向边的流量。不过,这样做的时间复杂度是 $O(mV)$ 的,原因还在上图中:如果最初选择了 $1\to 2\to 6\to 7$,接下来选择 $1\to 5\to 6\to 2\to 4\to 7$,那么会无限的重复下去直到 $10^9$ 变成 $0$,也就是说会进行 $2\times 10^9$ 轮增广。
这个也叫 FF 算法,时间复杂度是伪多项式的,这很不好,接下来探索一些多项式做法。
Edmonds-Karp
注意到,每次增广路的条件是任意的。也就是说,一个优化方向是限制每次选择增广路的条件,从而获得更优的复杂度。
EK 算法每次增广选择最短路径(即边数最小的路径),而如果这样做增广的次数便是 $O(nm)$ 的。
证明: 每次增广时,必然会在残量网络上删除一条边。那么,对于边 $(u,v)$,如果先后删除 $(u,v)$ 和 $(v,u)$ 意味着什么?令删除 $(u,v)$ 的时候,$d_u$ 和 $d_v$ 为 $s\to u$ 和 $s\to v$ 的最短路,删除 $(v,u)$ 的时候,$d_u'$ 和 $d_v'$ 为 $s\to u$ 和 $s\to v$ 的最短路。则有如下不等式: $$ d_u+1=d_v\lt d_v'+1=d_u' $$ 根据传递性,不难得到 $$ d_u+2\le d_u' $$ 也就是说,对于每条边,至多删除 $\frac{n}{2}$ 次,总共有 $m$ 条边,则至多进行 $O(nm)$ 次增广。每次增广需要进行一次 BFS,所以说时间复杂度为 $O(nm^2)$。
【参考代码】
i64 EK(int s, int t) {
i64 res = 0;
while (1) {
memset(flow, -1, sizeof flow);
tt = 0, q[ ++ tt] = s, flow[s] = INT_MAX;
for (int i = 1; i <= tt; i ++) {
int u = q[i];
for (int j = h[u]; ~j; j = ne[j]) {
int v = e[j];
if (~flow[v] || !f[j]) continue;
flow[v] = min(flow[u], f[j]);
q[ ++ tt] = v, pre[v] = j;
}
}
if (flow[t] == -1) break;
int cur = t, i;
while (cur != s) {
i = pre[cur], f[i] -= flow[t];
f[i ^ 1] += flow[t], cur = e[i ^ 1];
}
res += flow[t];
}
return res;
}
Dinic
EK 算法每次增广一条增广路,而 BFS 可以同时处理出多条最短路,形成最短路 DAG。在这张最短路 DAG 上,可以同时增广多条增广路,所以只需要找出最大的可能流的流量即可。
这个可以 DFS 求解,对于每个点存储前面最小的剩余容量,每次枚举邻边 $(u,v,w)$,并判断 $v$ 是否在下一层,转移过去即可(DFS(v, min(lim - flow, w)))。
当前弧优化:当 DFS 从 $u$ 到 $v$ 时,则这条边剩余容量会变成 $0$。那么,后面再到达 $u$ 的时候,找第一个剩余容量不为 $0$ 的边,可以通过记录当前弧,从而找到第一条剩余容量不为 $0$ 边做到 $O(1)$。
这样,增广的次数是 $O(n)$ 的,因为每增广一次,会导致 $s\to t$ 的最短路至少增加 $1$,因为如果最短路不变,则可以多流一条增广路。DFS 的时间复杂度是 $O(nm)$ 的,因为每次 DFS 到 $t$ 会导致一条边删除,而至多只有 $m$ 条边,每次删除一条边至多经过 $n$ 个点。
综上,时间复杂度为 $O(n^2m)$,常数很小。
【参考代码】
bool bfs() {
memset(dist, -1, sizeof dist);
tt = 0, q[ ++ tt] = s, dist[s] = 0;
for (int i = 1; i <= tt; i ++) {
int u = q[i];
cur[u] = h[u];
for (int j = h[u]; ~j; j = ne[j]) {
int v = e[j];
if (~dist[v] || !f[j]) continue;
dist[v] = dist[u] + 1;
q[ ++ tt] = v;
}
}
return ~dist[t];
}
i64 dfs(int u, i64 lim) {
if (u == t) return lim;
i64 flow = 0;
for (int i = cur[u]; ~i && flow <= lim; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (dist[v] == dist[u] + 1 && f[i]) {
i64 t = dfs(v, min(lim - flow, (i64)f[i]));
flow += t, f[i] -= t, f[i ^ 1] += t;
}
}
return flow;
}
i64 dinic() {
i64 res = 0;
while (bfs()) res += dfs(s, LONG_LONG_MAX);
return res;
}
最小费用最大流
如今有费用,那么直观上的方式是每次增广费用和最小的路径,这样才是最优的。事实也确实如此,证明略,感兴趣的读者可以自行上网查找。
所以,每次只需要将 EK 中的 BFS 替换成 SPFA(注意有负边权,因为需要考虑反向边),时间复杂度 $O(nmf)$。因为每次选择费用和最小的路径,会导致并没有很好的性质,很容易卡到 $O(f)$ 次增广。SPFA 的时间复杂度为 $O(nm)$,故总复杂度为 $O(nmf)$。
该算法称之为 Successive Shortest Path,简称 SSP,业界公约。实现是简单的,参考代码略。
上下界网络流
无源汇上下界可行流
问题描述: 给定一张 $n$ 个点 $m$ 条边的网络,每条边有流量下界和上界,试求任意一个可行流。
如果有下界怎么办?考虑强制选择下界,容量变成上界 $-$ 下界(即流 $x$ 的流量等价于原图流 $x+\text{low}$ 的流量),但是问题在于下界不一定是流量守恒的。
于是,考虑进行补流。建立超级源点 $s$ 和超级汇点 $t$。对于点 $u$ 来讲,如果入的比出的多,则从 $u\to t$ 连接一条容量为差值的边;如果入的比出的少,则从 $s\to u$ 连接一条容量为差值的边。
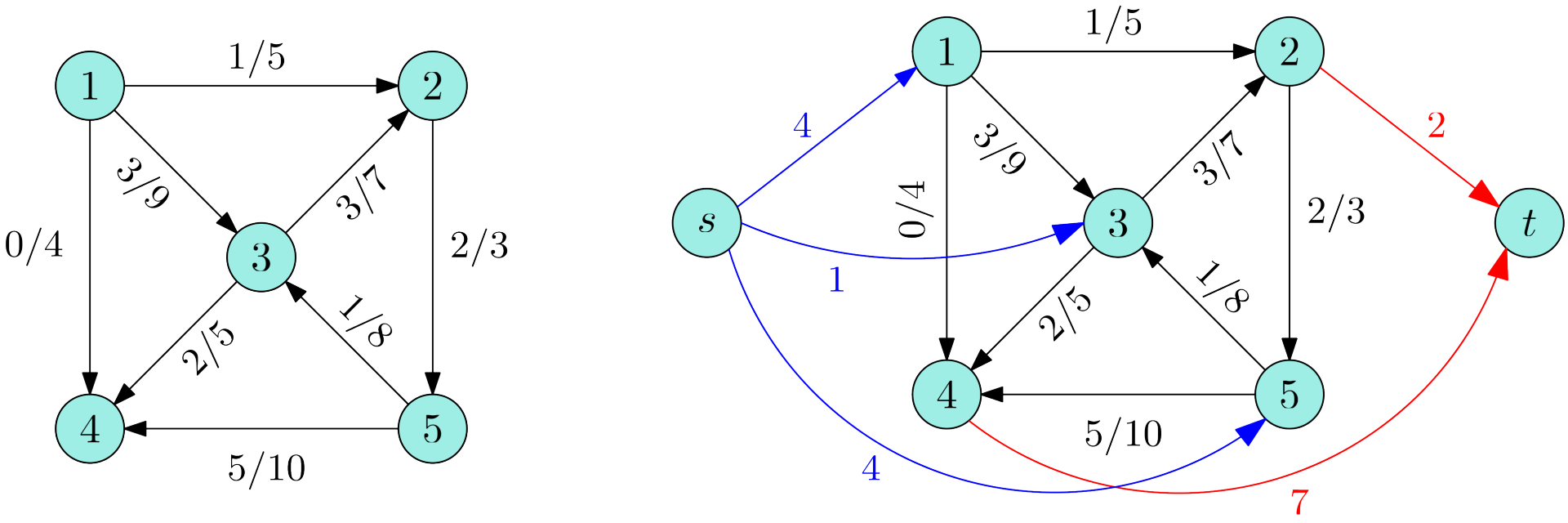
由于 $s$ 与原图中的点只有补流的边,原图中的点到 $t$ 只有补流的边,所以必然将补流的边流满,为了流量守恒,也就导致原图中的边提高对应的流量。
【参考代码】
const int maxn = 205;
int n, m;
int diff[maxn];
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> m;
maxflow<int> mf(n + 1);
std::vector<array<int, 3>> edge;
for (int i = 1; i <= m; i ++) {
int u, v, lo, hi;
cin >> u >> v >> lo >> hi;
diff[u] += lo, diff[v] -= lo;
mf.add(u, v, hi - lo);
edge.push_back({u, v, lo});
}
for (int i = 1; i <= n; i ++)
if (diff[i] > 0) mf.add(i, n + 1, diff[i]);
else if (diff[i] < 0) mf.add(0, i, -diff[i]);
mf.dinic(0, n + 1);
for (int i = 2 * m; i < mf.idx; i += 2)
if (mf.f[i]) {
cout << "NO" << endl;
return 0;
}
cout << "YES" << endl;
int id = 1;
for (auto [u, v, w] : edge) {
cout << mf.f[id] + w << endl;
id += 2;
}
return 0;
}
有源汇上下界最大流
有源汇上下界可行流是简单的,这里直接讨论最大流的求解。沿用 $2.1$ 中强制选择 $\text{low}$ 的思路,把每条边的流量变成 $\text{low+x}$,容量为 $\text{high}-\text{low}$。
考虑如何将 $\text{low}$ 平衡,将有源汇转化为无源汇,只需要 $t\to s$ 连接一条容量为 $\infty$ 的边。接下来,按照无源汇上下界可行流的求解方式求出一张可行流。
在任意可行流上,继续跑 dinic 仍然可以求解出最大流,因为相当于每条边 $(u,v)$ 可以增加 $c(u,v)-f(u,v)$ 的流量,也即剩余容量为 $c(u,v)-f(u,v)$;可以减少 $f(u,v)$,也即反向边的剩余容量为 $f(u,v)$,这与该可行流的残量网络是一致的。所以只需要在这张可行流上从 $s\to t$ 跑一遍 dinic 即可。
【参考代码】
const int maxn = 205;
int n, m, s, t;
int diff[maxn];
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> m >> s >> t;
maxflow<i64> mf(n + 1);
for (int i = 1; i <= m; i ++) {
int u, v, lo, hi;
cin >> u >> v >> lo >> hi;
mf.add(u, v, hi - lo);
diff[u] += lo, diff[v] -= lo;
}
mf.add(t, s, INT_MAX);
for (int i = 1; i <= n; i ++)
if (diff[i] > 0) mf.add(i, n + 1, diff[i]);
else if (diff[i] < 0) mf.add(0, i, -diff[i]);
mf.dinic(0, n + 1);
for (int i = 2 * m + 2; i < mf.idx; i += 2)
if (mf.f[i]) {
cout << "please go home to sleep" << endl;
return 0;
}
cout << mf.dinic(s, t) << endl;
return 0;
}
有源汇上下界最小流
最小流与最大流的求解方式极为类似,核心思想不变:先求解可行流,将 $\text{low}$ 平衡。接下来,求解该流基础上的最小流。
第一步与最大流完全一样,这里不再赘述。考虑现在求解出一张平衡 $\text{low}$ 的可行流,接下来如何求解最小流。相当于边 $(u,v)$ 剩余容量为 $f(u,v)$,反向边剩余容量为 $\text{high}(u,v)-\text{low}(u,v)-f(u,v)$,不难发现,这相当于把之前建的反向边当正向边,正向边当反向边,也就是 $t\to s$ 的最大流。
注意:在求 $t\to s$ 最大流的时候,需要将 $t\to s$ 边删除。
【参考代码】
const int maxn = 50005;
int n, m, s, t;
i64 diff[maxn];
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> m >> s >> t;
maxflow<i64> mf(n + 1);
for (int i = 1; i <= m; i ++) {
int u, v, lo, hi;
cin >> u >> v >> lo >> hi;
mf.add(u, v, hi - lo);
diff[u] += lo, diff[v] -= lo;
}
mf.add(t, s, INT_MAX);
for (int i = 1; i <= n; i ++)
if (diff[i] > 0) mf.add(i, n + 1, diff[i]);
else if (diff[i] < 0) mf.add(0, i, -diff[i]);
mf.dinic(0, n + 1);
i64 res = mf.f[2 * m + 1];
for (int i = 2 * m + 2; i < mf.idx; i += 2)
if (mf.f[i]) {
cout << "please go home to sleep" << endl;
return 0;
}
mf.f[2 * m] = mf.f[2 * m + 1] = 0;
cout << res - mf.dinic(t, s) << endl;
return 0;
}





 鲁ICP备2025150228号
鲁ICP备2025150228号