本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-13 20:01:47

虽然标签给的是拓扑排序，但是本题实际上可以看成是联通性问题。

一头牛的排名能够确定，当且仅当它与其他所有奶牛都能够比较出优劣。也即，在图中，它需要与其他所有奶牛都联通。

题目便是统计这样的点的数量。

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-13 21:12:18

图的割点

割点可以理解为是图中这样一种点：去掉它之后，原来的图割成了更多个子图，也即，这个图的极大连通分量数增加了。

图的割点可以用暴力的方法求得：遍历每一个点，删除并计算新的连通分量数。当然这个方法就跟它看起来那样愚蠢。

求图的割点可以使用 Tarjan 算法。

Tarjan 算法的分析

Tarjan 算法是类似 DFS 的算法：它对每一个点计算两个值，low 和 dfn。

其中 dfn 是这个点的访问顺序，类似树的深度；而 low 是这个点所连接到的最高的点的 dfn（当然不包括它的父亲）。

通过这两个数据，我们怎么判断一个点是不是割点呢？

low 是关键。

low 的实质是某个点所能连到的最高祖先。对于一个点 A，如果它的一个孩子 B 能够连接到比 A 更高的点，即 low[b] < dfn[a] 那么明显删除了 A 对 B 没有任何影响，因为 B 可以通过 low 中存储的祖先来与图联通。

但是如果 low[b] >= dfn[a]，也就是说 B 不能连接到比 A 更高的点，那么把 A 删除，明显会让 B 和整个图断开连接。所以，只要存在这样的孩子点，A 就是一个割点

（B：A，至少对我来说，你是不可或缺的）。

Tarjan 算法的实现

自然是 DFS。以 P3388 【模板】割点（割顶） 为例。

存图用邻接链表即可。之后对每一个没有访问过的点 i （vis[i] == false），我们进行一次 Tarjan（因为题目中提到本图不一定联通）。

DFS 中先设置 vis 和 dfn，然后将 low 初值设为 dfn。然后对每一个孩子进行 DFS，同时若孩子能连到比自己更高的点，便更新 low 与孩子的 low 相同。

之后我们判断是否是割点：如果 low[t] >= dfn[u] 并且这个点没有被找到过（因为我们需要进行多次 Tarjan，防止重复计算）我们就更新割点数量。

这里和普通 DFS 有一点不同：当孩子已经被访问过时，我们也需要对其处理，以更新 low 值。

同时还需要注意一点：

开始 Tarjan 的点需要进行特判，但也十分简单。我们知道，只要它有两个以上孩子，那么它一定是割点（因为起始点的入度是为零的）

以上就是 Tarjan 算法求割点的具体步骤。代码可参考 OI Wiki。

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-14 10:18:57

题意就是求一个图中的最小环。但本题的边有很大的特殊性，因此可以用并查集完成。

有怎样的特殊性？

—— 本题中一个点最多有两条边相连，一条出边一条入边。所以可以用并查集解决。

并查集可以轻松判断是否形成环。但是要怎样计算环的长度？

实际上当一个点 A 在这个图（并查集）中形成环的时候，这个环的长度就是它到祖先的距离， find 过程递归的次数。

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-14 10:40:27

本题虽然没有图，但是是明显的图论题。一只猴子想要到达所有的树，当且仅当它的跳跃能力要大于等于到所有树的最大距离。

这个“到所有树的最大距离”，很明显是最小生成树。

于是求出最小生成树，并且维护最大距离。之后对每一个猴子进行比较即可。

复杂度 $O(N^2 + M)$。

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-14 11:36:38

最开始考虑的是把 dis 初值设为挖井的代价，还兴致勃勃打了一大堆 Prim，最后发现狗屁不通。

看了一眼第一篇题解茅塞顿开。我们可以将“挖井”的操作看成是与地下相连。权重就是挖井的代价。Kruskal 即可。

本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2023-12-14 13:04:04

乍看本题以为是二分，但正解实际上是 MST。

“部落” 实际上就是连通块，而本题所要求的就是让连通块之间的路径最大（两个最近的部落之间尽可能远离）。

我们可以求这个图的最小生成树，这样，这棵 MST 中前 k 大的边就是所要断开的部落之间的路径。所以，这前 k 大的边中最小的也就是整个 MST 的边中的第 k - 1 大的边。

在 Prim 中维护所生成的 MST，最后输出第 k - 1 大即可。

我有一车对 WyOJ 的设想。很多可以实现，很多很难实现，很多我想实现，很多我不怎么想实现。

• 有一个可以实时预览的 Markdown 编辑器。难度不算太高，但是需要学现在 UOJ 用的这套前端框架，我没啥兴趣

• 评论可以用 Markdown 等。同理，难度不算很高，但是我不想学 marked 与 MathJax 怎么用，我对前端有零个兴趣。也许以后某天闲的时候会做

• 热全量备份系统。WyOJ 到现在只有一个本地的温数据库备份系统和冷数据备份系统（刻到光盘），我想做一个热全量备份系统。难度不高，我计划用 Glusterfs，但是发现 Alpine 没有 Glusterfs，于是暂时搁置。

• 博客的预览。很简单，只是懒得写。

• WyOJ 一车小功能 fix。太杂太麻烦，没有修复的欲望。

• 将洛谷专栏导入到 WyOJ。这个我非常想做，且正在做。具体方案是用开源的保存站（luogu-server）部署到本地来完成。正在学习。

• 与 CF、AtCoder 等联动。这个也很想做，但是还没有认真学习 Codeforces / Atcoder API，所以暂时没有能力。

• 接入一个基于深度学习的题目推送网络。这个项目是商业级的，我如果能把这玩意儿做好了，估计一大段时间不用打工了。但是我还没有学深度学习，正在买书 + 学习。

• 还有很多架构上的更新，太冗杂，没有兴趣。

大家谁如果有兴趣修复这些问题，可以联系我。

哪些博客优先得到推荐呢？

• 经久不衰：也就是得到赞与评论相当多的

• 后起之秀：赞与评论还没有很多但是增长速度快的（根据 post_time）

• 新作：要给予新作一定的曝光机会

先把功能做好，然后再做推荐。

整理了一些关于 Splay 的资料，一个简洁美丽而高效的数据结构。

Splay 是最简洁的平衡树之一，支持维护区间信息。相比线段树，其可以动态地删点、加点，更加灵活；相比分块，其复杂度是均摊对数，更加高效。

在形态变化时，Splay 并不通过维护一系列性质来保证树高，而是通过伸展保证均摊复杂度。这让它少了常见平衡树的繁杂分讨，但常数也要大不少。

形态及操作

Splay 首先是一棵二叉搜索树，由许多节点组成。我们在每个节点维护父亲的左右儿子指针，以及键值。如有需要，还可以维护它子树内的信息，如它的子树大小。维护子树大小，可以实现快速查询第 k 大或者某数排名。

Splay 的核心操作是伸展（splay）。伸展某个节点 $x$，意味着将 $x$ 节点提升到根，同时更新所维护的子树信息。原来的根在伸展后成为某个普通内部节点。伸展操作的均摊复杂度是对数。

如果能够实现伸展操作，就可以方便地进行许多操作：

• 插入。插入与普通二叉树的插入相同，按照二叉树的遍历方法找到某个叶子节点，将新值插入到该叶子的儿子下。不同的是，在插入某个点后，为了保证复杂度正确，我们要将这个节点伸展到根。

• 删除。首先将这个节点伸展到根，然后将其与其儿子断开。这时原树分裂成两个子树，考虑合并它们。找到左子树的最大值，由二叉树的性质，这个数一定小于右子树的最小值。因此，我们将 $y$ 伸展到根。这时 $y$ 的右儿子一定空，于是将右子树拼到其右儿子上即可。

• 查找某个数。按照二叉树的查找方法，一直找到这个数，或者某个叶子。将最后找到的节点伸展到根。

• 查询排名。首先查找这个数，伸展到根。然后小于其的数数量就是现在根左子树的大小。如果待查询的值不存在，还要考虑根是否小于这个数。

• 查询第 $k$ 大。和二叉树相同。从根节点开始遍历。如果当前节点 $x$ 左子树的大小，也就是小于 $x$ 的数字数量，大于等于 $k$，要找的节点在左子树；如果等于 $k - 1$，那么就是当前节点 $x$；否则，在右子树，并且 $k$ 减去左子树加上当前点大小。

• 查询前驱。伸展到根，然后找左子树的最大值，也就是一直向右走。如果查询的值不存在，特判根是否小于待查值。

• 查询后继。与查询前驱同。

• 查询区间。设待查询区间为 $[l, r]$，我们将 $l - 1$ 旋到根，$r + 1$ 旋到根的右儿子，那么根的右儿子的左儿子，其上的信息就是 $[l, r]$ 的信息。

伸展

旋转

现在，我们只需要有效地实现伸展操作，就可完成所需的一切操作。

考虑怎么将某个节点高度提升一。我们称这个操作为旋转。

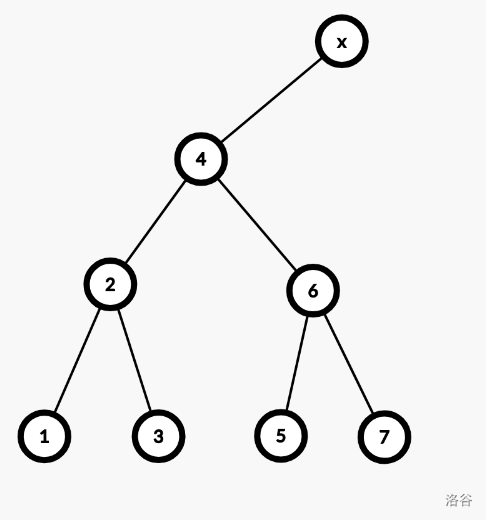
考虑怎么将 $2$ 提升到 $4$ 的位置。

那样，$4$ 该放到哪里？可以接到 $2$ 的右儿子上。$2$ 的右儿子放到哪里？放到 $4$ 的左儿子上，因为 $4$ 原来的左儿子是 $2$，现在已经空。其他子树不变。因此，变的只有 $2$ 和 $4$。

单旋与双旋

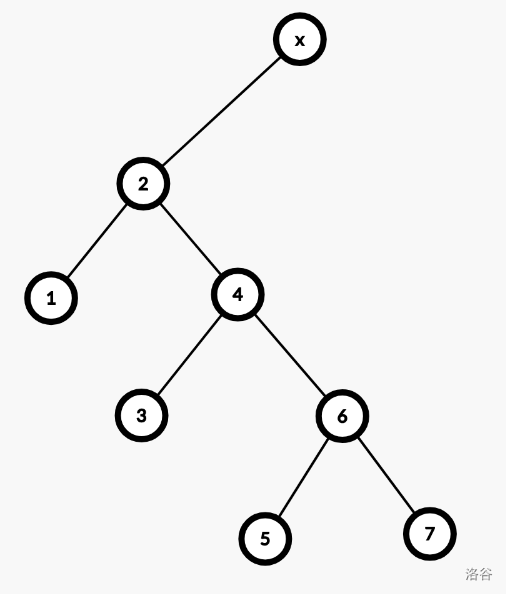
伸展操作能不能直接一直向上旋转呢？可以，但复杂度错误。

为了改善复杂度，我们需要引入双旋。

双旋是指，在伸展过程中，如果出现 $x$ 与 $x$ 的父亲同向，不能简单地旋转两次 $x$，而是要先旋转其父亲，再旋转 $x$。

我们如果想要将 $6$ 伸展到根，是不是需要双旋？答案是肯定的，因为 $4$ 和 $6$ 都是其父亲的右儿子，属于同向。如果是伸展 $3$，就不需要了。按照双旋的过程，我们先旋转 $4$，再旋转 $6$。也就是，先变成：

后旋转 $6$

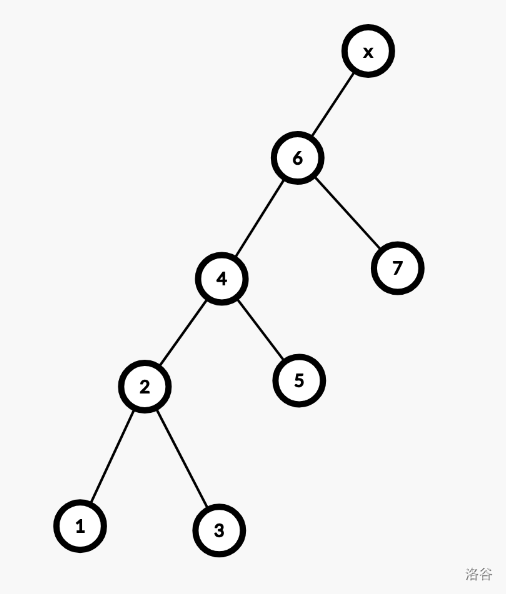
光看上图，可能感觉双旋和单旋没有什么区别，但实际上在复杂度分析时，使用双旋可以保证某个性质，进而保证复杂度正确。

总之，我们已经知道了怎样以正确的复杂度将 $x$ 伸展到根。有关 Splay 的基本操作，就介绍完毕了。

附一份常数和美观程度都不错的实现。

复杂度

势能分析简介

我们发现，Splay 的复杂度来源于两部分，一部分是遍历，另一部分是伸展。让最终遍历到节点马上被伸展到根，就可以把复杂度都算在伸展里，进而只需证明伸展的复杂度。

我们采用势能分析。势能分析是指，引入某个势能函数 $\Phi(D)$，描述某时数据结构的状态。

设每次操作的代价是 $c_i$，每次操作后数据结构为 $D_i$。要证 $\sum c_i$ 有某上界。如果 $\Phi(D_n) - \Phi(D_0) = O(F(n))$，$\Phi(D_n) - \Phi (D_0) + \sum c_i = \sum (c_i + \phi(D_i) - \phi(D_{i - 1})) = O(G(n))$，显然 $\sum c_i = O(F(n) + G(n))$。

这样有什么好处？我们考虑，Splay 等数据结构复杂度分析的难处，在于我们只知道 $c_i$ 的一个很松的上界，而不好直接分析 $\sum c_i$。实际上，某个大的 $c_i$ 对数据结构的影响也是大的，会导致后续的操作 $c_i$ 更小；换句话说，不会出现所有 $c_i$ 都取到上界的情况。

引入势能函数后，每个很大的 $c_i$，可以用一个很小的 $\Phi(D_i) - \Phi(D_{i-1})$ 来平衡。因而可以更方便地放缩，并得到上界。

具体分析

我们设某个节点的势能函数为 $\phi(x) = \log \lvert x\rvert$（$\log$ 均以二为底；$\lvert x\rvert$ 表示 $x$ 的子树大小），$\Phi(D) = \sum \phi(x)$。显然的，$0\le \Phi(D) \lt n\log n$，并且 $\Phi(D_n) - \Phi(D_0) = O(n\log n)$。我们要证明每次伸展操作的均摊复杂度是对数。

伸展的分解

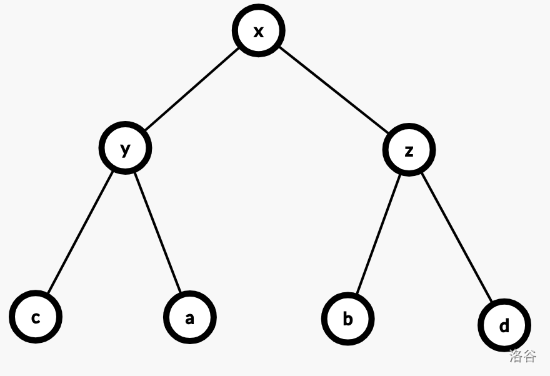
根据上面对 Splay 的介绍，我们可以将伸展分为三种具体操作。设 $x$ 为待伸展的节点，$y$ 为 $x$ 的父亲，$z$ 为 $y$ 的父亲。

• zig，即一次单旋，在 $y$ 为根时候发生。直接旋转 $x$，其深度减少一。发现这种旋转最多发生一次。

• zig-zig，即一次双旋，在 $y$ 和 $x$ 同向时发生。先旋转 $y$，后旋转 $x$。$x$ 深度减少二。

• zig-zag，即两次对 $x$ 的单选，在 $x$ 和 $y$ 不同向时发生。$x$ 深度减少二。

伸展的过程是数次 zig-zig 与 zig-zag 的组合，加上可能存在的一次 zig。

zig 的分析

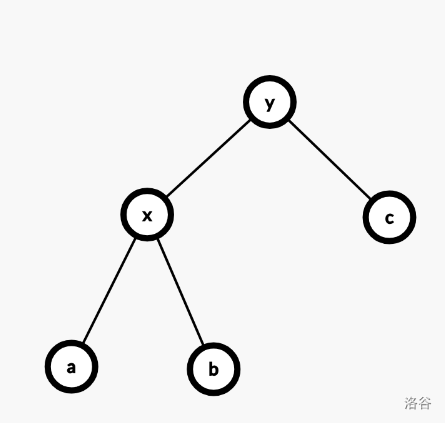
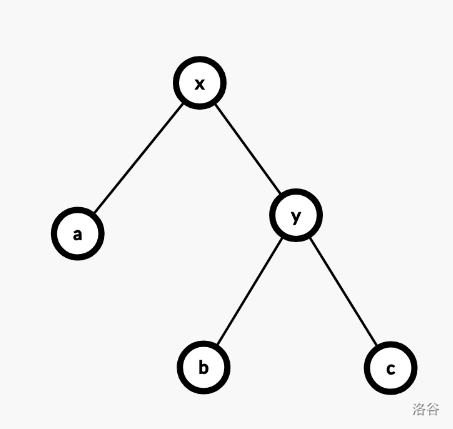
旋转的复杂度为 $O(1)$，势能的变化量为

$\phi(x') + \phi(y') - \phi(x) - \phi(y) = \phi(y') - \phi(x) \le \phi(x') - \phi(x)$

因此摊还代价是 $O(1) + \phi (x') - \phi (x)$。

zig-zig 的分析

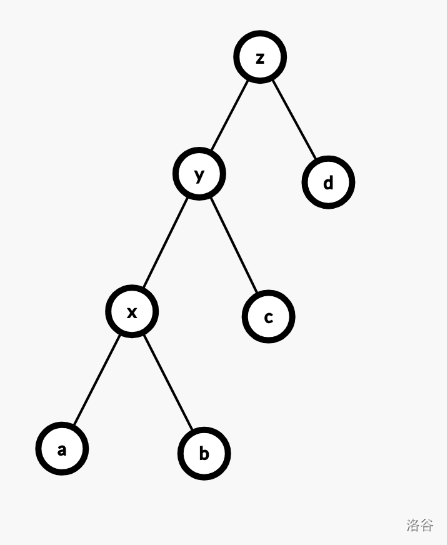
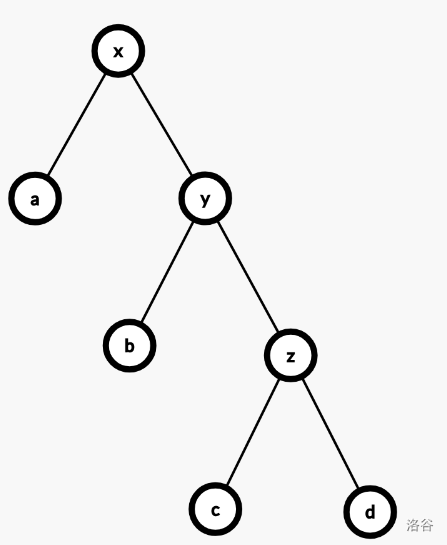
摊还代价是

$$ \begin{aligned} & c \\ =& 1 + \phi(x') + \phi(y') + \phi(z') - \phi(x) - \phi(y) - \phi(z) \\ =& 1 + \phi(y') + \phi(z') - \phi(x) - \phi(y) \\ \end{aligned} $$

考虑怎么把 $1$ 去掉，因为如果引入 $1$，就会导致最终复杂度与旋转次数有关。

有：

$$ \begin{aligned} 2\phi(x') - \phi(x) - \phi(z') = \log (\dfrac{\lvert x'\rvert^2}{\lvert x\rvert\lvert z'\rvert}) \ge 1 \end{aligned} $$

这是因为 $\lvert x'\rvert \ge \lvert x\rvert+\lvert z'\rvert$。注意到不双旋时，此不等式不满足。这也是为什么双旋才能保证复杂度。

用这个不等式代换常数 $1$，得到

$$ \begin{aligned} & c \\ \le& 2\phi(x') - \phi(x) - \phi(z') + \phi(y') + \phi(z') - \phi(x) - \phi(y) \\ \le& 2\phi(x') - 2\phi(x) + \phi(y') - \phi(y) \\ \le& 3\phi(x') - 3\phi(x) \\ =& O(\phi(x') - \phi(x)) \end{aligned} $$

成功将常数消去，同时和前面的 $\phi(x') - \phi(x)$ 保持了一致。

zig-zag 的分析

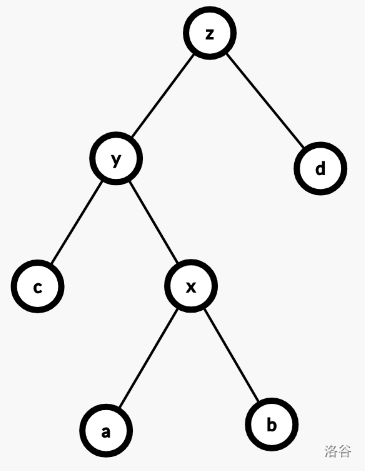
类似的，我们有不等式：$2\phi(x') - \phi(y') - \phi(z') = \log (\dfrac{\lvert x'\rvert^2}{\lvert y'\rvert\lvert z'\rvert})\ge 1$

$$ \begin{aligned} & c \\ &= 1 + \phi(x') + \phi(y') + \phi(z') - \phi(x) - \phi(y) - \phi(z) \\ &= 1 + \phi(y') + \phi(z') - \phi(x) - \phi(y) \\ &\le 2\phi(x') - \phi(y') - \phi(z') + \phi(y') + \phi(z') - \phi(x) - \phi(y) \\ &\le 2\phi(x') - 2\phi(x) - \phi(y) \\ &\le 2\phi(x') - 2\phi(x) \\ &= O(\phi(x') - \phi(x)) \end{aligned} $$

综合

分析得到，zig 的摊还代价为 $O(1 + \phi(x') - \phi(x))$，而这种旋转最多一次；其他的两种旋转，摊还代价都是 $O(\phi(x') - \phi(x))$。这样，伸展的总代价就是 $O(\log \lvert x'\rvert - \log \lvert x\rvert + 1) = O(\log n)$。我们成功证明了伸展的复杂度是摊还对数，由此知道 Splay 的复杂度是正确的。

如题！

参加过两场及以上比赛且绑定了 QQ 的用户，可以在 WyOJ 用户激活群中 @ryp 来申请一个勋章。我看到后会颁发。

一个人可以有很多的勋章，可以点击右上角的“勋章管理”来选择展出的勋章。