本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2024-04-10 12:08:45

给定长为 $N$ 的两个整数列 $A$ 与 $B$，对于每个 $k = 1, 2, \cdots, N$，选择 $k$ 个互异下标组成集合 $S$，使 $(\sum\limits_{i\in S} A_i) - \max\limits_{i\in S}B_i$ 最大。

输出每个 $k$ 对应的最大值。

我用的是 $O(n\log^2 n)$ 的主席树 + 决策单调性分治，但是听说有单 $\log$ 的做法。

考虑 $k$ 固定的情况。我们枚举一个 $d\in [k, n]$ 作为 $\max B$ 的下标（先以 $B$ 为关键字排序），那么那个式子的最大值，显然是取 $k - 1$ 个最大的 满足 $B$ 小于 $B_d$ 的 $A$ 值之和。因为我们已经按照 $B$ 排序，那么就是取 $d$ 之前的 $k - 1$ 个最大 $A$ 值。明显主席树维护。

接下来观察单调性。一图胜千言，下面是 $k$ 与决策点的关系：

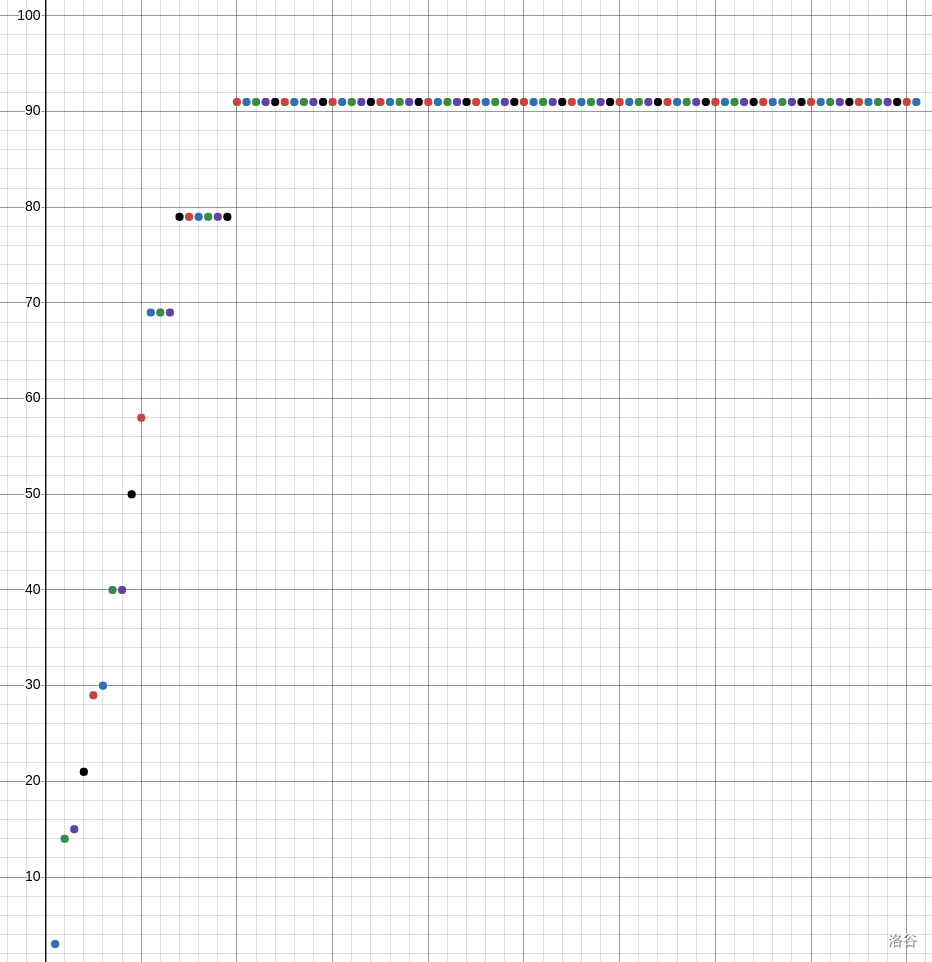
于是，$k$ 的决策点一定不高于 $k + 1$ 的，也不低于 $k - 1$ 的。这时，我们可以用决策单调性分治来得到 $[1, n]$ 上每个最大值。

最终复杂度是 $T(n) = T(\dfrac n 2) + O(n\log n) = O(n\log^2n)$ 的。

代码：

#include <iostream>
#include <algorithm>
#define int long long
#define fi first
#define se second
using namespace std;
using ll = long long;
using pi = pair<ll, ll>;
const int N = 2e5 + 10;
const ll inf = 1e18;
int qcnt[32 * N], qsum[32 * N], ls[32 * N], rs[32 * N], rt[N], cnt = 0, nr = 0;
ll dsc[N], f[N];
pair<ll, ll> z[N];

static inline ll J (ll x) { return dsc[nr++] = x; }
static inline int Q (ll x) { return lower_bound (dsc, dsc + nr, x) - dsc + 1; }

void upd (int &u, int v, int x, int y, int k, ll val)
{
    int mid = (x + y) \/ 2;
    qcnt[u = ++cnt] = qcnt[v] + 1, qsum[u] = qsum[v] + val, ls[u] = ls[v], rs[u] = rs[v];
    if (x == y) return;
    if (k <= mid) upd (ls[u], ls[v], x, mid, k, val);
    else upd (rs[u], rs[v], mid + 1, y, k, val);
}

ll qry (int u, int x, int y, int k)
{
    int mid = (x + y) \/ 2;
    if (x == y) return dsc[x - 1] * k;
    if (k <= qcnt[rs[u]]) return qry (rs[u], mid + 1, y, k);
    else return qry (ls[u], x, mid, k - qcnt[rs[u]]) + qsum[rs[u]];
}

void solve (int l, int r, int ql, int qr)
{
    int mid = (ql + qr) \/ 2, mpos = -1;
    ll mval = -inf;

    if (l > r || ql > qr) return;
    for (int d = max (l, mid); d <= r; d++) {
        ll f = qry (rt[d], 1, nr, mid) - z[d].se;
        if (f > mval) mval = f, mpos = d;
    }

    f[mid] = mval;
    solve (l, mpos, ql, mid - 1), solve (mpos, r, mid + 1, qr);
}

signed main (void)
{
    int n;

    ios::sync_with_stdio (false), cin.tie (0), cout.tie (0);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> z[i].fi >> z[i].se, J (z[i].fi);
    sort (z + 1, z + n + 1, [](pi &x, pi &y) { return x.se < y.se; }), sort (dsc, dsc + nr), nr = unique (dsc, dsc + nr) - dsc;
    for (int i = 1; i <= n; i++) upd (rt[i], rt[i - 1], 1, nr, Q (z[i].fi), z[i].fi);
    solve (1, n, 1, n);
    for (int i = 1; i <= n; i++) cout << f[i] << '\n';
    return 0;
}