本文章由 WyOJ Shojo 从洛谷专栏拉取，原发布时间为 2025-10-15 15:07:45

P5994 [PA 2014] Kuglarz 题解

P5994 [PA 2014] Kuglarz - 洛谷

确实是一道非常深刻的题目。

感觉其他题解都没有讲出要点，或者讲明白我的疑点，于是记录下来，希望有所帮助。

题解主要说明了，如何想到建图，以及如何把区间询问问题转化为前缀问题，再转化成最小生成树的问题。

先来看这个问题

你有一个序列 $A$，现在你知道 $n$ 个区间 $[l,r]$ 的区间和。

同时给出 $Q$ 次询问，问你能否根据给出的 $n$ 个提示，求出 $\sum_{i = 1}^{x} a_i$ 的值，输出 yes 或 no。

我们考虑把给出的区间和转化为前缀和。设 $pre_i = \sum_{j = 1}^{i} a_j$，其中我们已知 $pre_0 = 0$。每次给出的信息相当于是给出 $pre_r - pre_{l - 1}$，于是我们只要知道了 $pre_{l - 1}$ 或 $pre_r$ 中的一个，就可以推出另一个。

我们将相互可以推出的 $pre$ 看作点，将给定的操作看作边，连边之后，同一连通块内的点可以相互推出值。

比如给出下面三个区间：

1 2
2 3
2 2

我们可以得到这样的图：

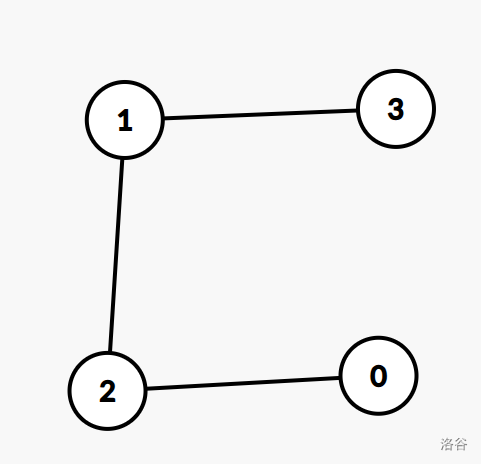
当知道了 $pre_0$，就可以知道 $pre_2,pre_3,pre_1$，发现这个东西可以使用并查集维护，位于同一集合内的点可以相互推出值。

这段参考了 (前缀和/并查集)代码源每日一题 Div1 区间和 - 知乎，并对题面进行了一点修改。

问题中的操作和建图有什么关系

看完前面的题目，好像和这道题目并没有什么关系。但我们发现，询问奇偶性的操作其实可以看作一段区间的异或值。也就是在下文中，奇偶性和异或和实际上是等价的。

设 $A_i = 0/1$ 表示第 $i$ 个杯子中有（没有）球，那么在本题中我们询问一个区间奇偶性相当于知道了区间异或和（这里可以自己思考一下）。

这里就解释了我不理解的第一个问题，为什么区间询问问题可以转化为前缀询问？

联系到上一题上，发现区间异或和操作可以转化为前缀异或和操作，令 $B_i = \oplus_{j = 1}^{i} A_j$，即前缀异或和，那么本题中一次询问就变成了上一题中给定的一个提示，询问 $[l,r]$ 后,在图上 $l - 1$ 与 $r$ 就联通了，也就是在图上 $l - 1$ 和 $r$ 之间连一条边。

我们考虑对于 $i$ 位置，想知道它有没有球，必须要选择一个 $j$，询问区间 $[j,i]$ 和区间 $[j,i - 1]$ 的异或和（这里应该是好理解的）。

发现询问区间 $[j,i]$ 的答案实际上就是询问 $B_i \oplus B_{j - 1}$，而 $[j,i - 1]$ 实际上就是询问 $B_{i - 1} \oplus B_{j - 1}$，我们只关心这两个的值是否相同，如果相同则 $i$ 没有球，否则有球。

以及第二个问题，为什么需要最小生成树？

由于只关心是否相同，所以两式子同时 $\oplus B_{j - 1}$ 是没有影响的。于是对于每个杯子 $i$ 求是否有球的过程，就转化为了询问 $B_i$ 与 $B_{i - 1}$ 的值，也就是我们需要求出每个 $B_i$。

换句话来说，想知道 $i$ 有没有球，最终都可以转化为询问 $B_i$ 和 $B_{i - 1}$ 的值，也就是我们需要在若干次询问之后做到能够知道 $B_i$ 和 $B_{i - 1}$ 的值。

由上一题我们已经知道，这样连边之后，对于同一连通块内的点可以相互求出值，也就是我们希望能把 $B_i(i \in [0,n])$ 连成一个连通块。

于是问题就转化完成了，即：

给定 $O(n^2)$ 条边，每条边 $(i - 1,j)$ 的边权为 $c_{i,j}$，需要找到一种最小花费使得 $0,1,2, \cdots ,n - 1,n$ 联通，于是把边存起来，做最小生成树就做完了。

#include<bits\/stdc++.h>
using namespace std;
#define int long long
struct note{
	int u,v,w;
}edg[4000010];
bool cmp(note x,note y) {return x.w < y.w;}
int fa[2010];
int getf(int x)
{
	if(fa[x] == x) return x;
	return fa[x] = getf(fa[x]);
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	int n;
	cin >> n;
	int cnt = 0;
	for(int i = 1;i <= n;i++)
		for(int j = i;j <= n;j++)
		{
			int w;cin >> w;
			edg[++cnt] = {i - 1,j,w};
		}
	sort(edg + 1,edg + cnt + 1,cmp);
	int ans = 0;
	for(int i = 1;i <= n;i++) fa[i] = i;
	for(int i = 1;i <= cnt;i++)
	{
		int u = edg[i].u,v = edg[i].v,w = edg[i].w;
		u = getf(u),v = getf(v);
		if(u == v) continue;
		fa[u] = v;
		ans += w;
	}
	cout << ans;
	return 0;
}

使用了 kruskal，可以修改成 prim。

希望对你有所帮助。

xuyunao 的博客

博客