本文章由 WyOJ Shojo 从洛谷专栏拉取,原发布时间为 2025-10-20 10:44:55
P12480 [集训队互测 2024] Classical Counting Problem 题解
P12480 [集训队互测 2024] Classical Counting Problem - 洛谷
题意
给定一棵 $n$ 个点的树,可以进行以下操作:
- 选择当前树上编号最大或最小的点,删除它以及以它为端点的所有边,并任选一个连通块作为新的树。
- 记 $min$ 为当前树上编号最小值,$max$ 为当前树上编号最大值,$size$ 为树上节点数量。定义一棵树的权值为 $max \times min \times size$,求能通过上述操作得到的非空树的权值和,答案对 $2^{32}$ 取模。
Solution
拿到题目,很难找到入手点,因此我们先来考虑一个性质:
- 一个 $min$ 和一个 $max$ 能够确定唯一的树。
我们考虑它的条件,$l,r (l \le r)$ 能确定一棵树的充要条件是,$l,r$ 路径上所有点编号都在 $[l,r]$ 之间。若不在则 $l,r$ 不能够作为 $min$ 和 $max$,否则可以从这条路径不断向外扩展,直到边界 $<l$ 或边界 $>r$,于是我们确定出一棵唯一的树。
此时我们容易得到一个 $O(n^3)$ 的做法,枚举 $l,r$,并 check $l,r$ 能否构成一棵合法的树。固定其中一个,移动另一个就可以做到 $O(n^2)$,可能需要带个 $\log$。
发现还需要继续优化,考虑拆贡献,可以将权值中的 $size$ 拆开,拆成对所有合法的 $(l,r,x)$ 三元组计算贡献,每个三元组的贡献就是 $l \times r$。问题转化为求树上有多少三元组 $(l,r,x)$,满足 $l,r$ 能确定一棵树并且 $x$ 位于 $l,r$ 确定出的树上。
考虑 $(l,r,x)$ 的关系大概是像下图中这样,按照 ez_lcw 课上讲的名字,称之为 “风车形”。
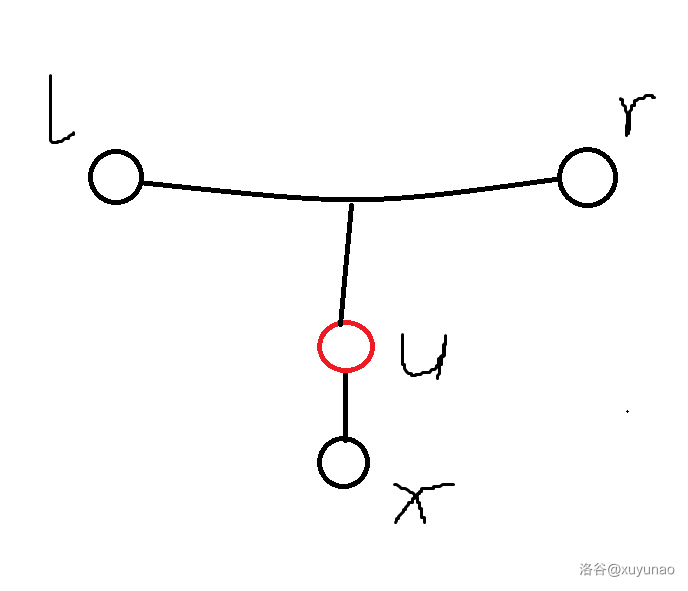
考虑点分治,对于每个风车,在风车上所有点中,点分树上深度最小的点上统计答案。假设红色点 $u$ 是统计答案的分治中心,需要满足 $l,r,x$ 均位于 $u$ 在点分树上的子树内,且其中至少两个点不在同一棵子树,也就是下图的两种情况。
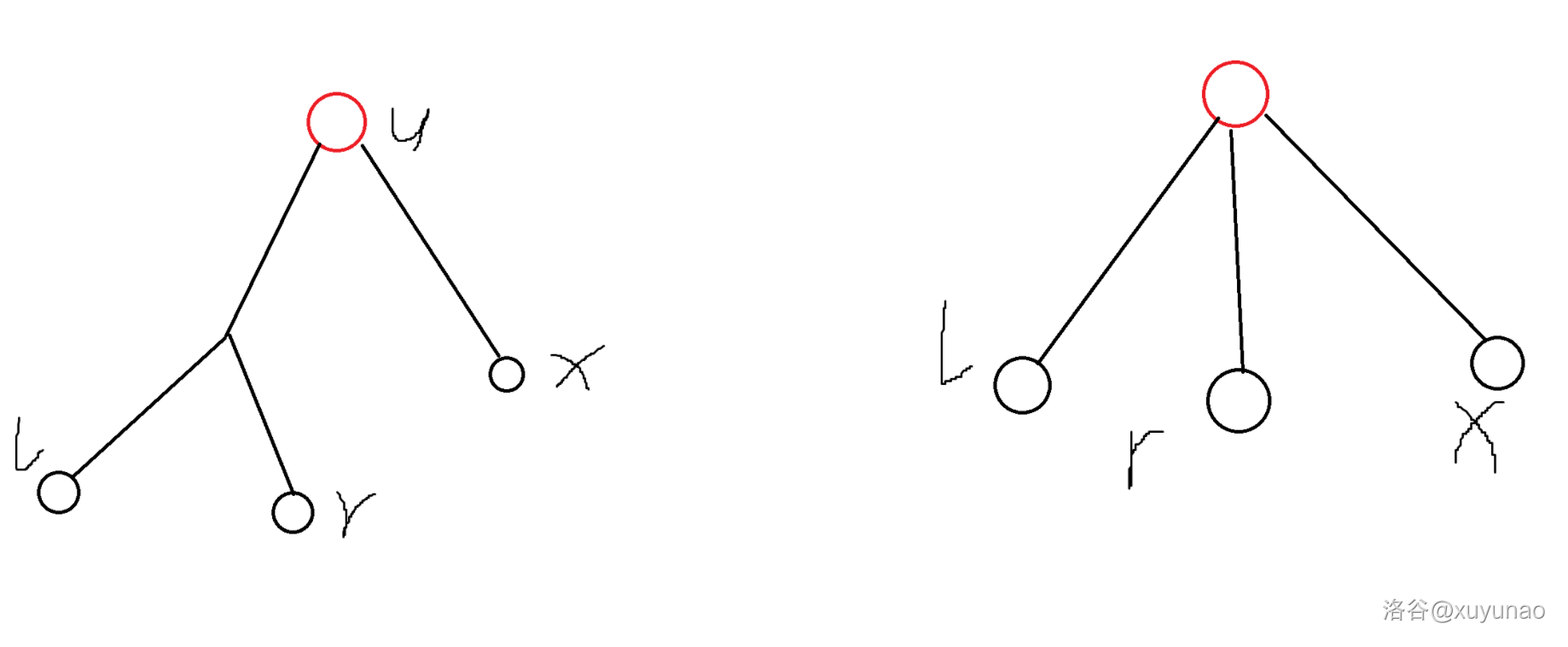
其中 $u$ 是这个风车上,点分树上深度最小的点。
接下来问题变成,我们如何统计子树内所有 $(l,r,x)$ 三元组的贡献,我们设 $mi_u$ 表示从分治中心到 $u$ 的路径上最小值,$mx_u$ 表示从分治中心到 $u$ 路径上的最大值,首先可以发现合法的 $l,r$ 满足 $mi_l = l,mx_r = r$。
$$\begin{cases} mx_l \le r \\ mx_x \le r \\ mi_x \ge l \\ l \le mi_r \end{cases}$$
考虑扫描线,对于每个 $r$ 处统计答案,统计合法的 $(l,x)$ 对的贡献。
考虑该怎么处理得到的限制关系。把子树内每个点 $u$ 维护在 $mx_u$ 的位置,从前往后扫描线,这样我们就解决了前两条限制关系。考虑维护一棵线段树,线段树需要维护三个信息:
- 对于每个位置 $i$,$l = i$ 的 $l$ 的编号和 $sum$。
- 对于每个位置 $i$,$mi_x = i$ 的 $x$ 的数量 $cnt$。
- 对于每个位置 $i$,$l = i$ 的合法 $(l,x)$ 对的贡献和 $val$。
那么对于每个限制 $4$,也就是 $l \le mi_r$,相当于是在一段前缀 $[1,mi_r]$ 查询合法 $(l,x)$ 对贡献,我们把拆完的贡献中的 $\times min$ 在这里计算。
接下来考虑如何统计 $(l,x)$ 对的数量,这里就要用到第三条限制关系,考虑加入一个点,这个点作为 $x$ 和作为 $l$ 的情况。
这个点作为 $x$,此时对于 $l \le mi_x$ 的所有 $l$,$x$ 都能与之配对产生贡献。对于所有合法的 $l$,它能增加的贡献值也为 $l$,要对这些 $l$ 的 $val$ 加上他们对应的 $sum$。同时插入 $x$ 后,$mi_x$ 处的 $cnt$ 也要 $+1$。
这个点作为 $l$,此时我们需要计算这个 $l$ 能和多少 $x$ 产生贡献,发现就是询问 $mi_x \ge l$ 的 $x$ 的数量,由于前面我们对每个位置 $i$ 维护了 $mi_x = i$ 的 $x$ 的数量,这里可以直接区间查询,同时 $l$ 位置的编号和也需要增加。
对于第一类,我们需要对贡献值区间加对应的 $val$,同时需要区间查询 $val$,因此需要线段树维护 $val$ 区间加,区间求和。同时需要对 $cnt$ 单点加,因此需要维护单点加的 $cnt$。
对于第二类,需要询问区间 $cnt$ 和,对 $cnt$ 线段树维护区间和,同时需要对 $sum$ 单点加,因此对 $sum$ 维护单点加区间查。
想通如何维护之后这道题目就很简单了,实现不难,维护出需要的信息即可。每层维护线段树,复杂度为 $O(m \log m)$,其中 $m$ 为点的数量,总复杂度 $O(n \log ^ 2 n)$。
实现细节
- 注意到模数是 $2^{32}$,可以直接使用 unsigned int 存储,这样就不需要取模了。
- 对于每层值域需要离散化,否则每层都是 $O(n\log n)$ 的,总时间复杂度会变成 $O(n^2 \log^2 n)$。
- 要先加入 $l,x$,再询问 $r$。
- 由于需要去重,如果对每棵子树减去贡献,注意路径 $\min$ 和 $\max$ 的初始值。
- 该清空的要清空,该赋值的要赋值。
代码(常数巨大)
#include<bits\/stdc++.h>
using namespace std;
#define int unsigned int
int n,ans,rt,tot;
const int maxn = 1e5 + 10;
bool vis[maxn];
vector<int> G[maxn];
inline int read()
{
int x = 0,f = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-') f = -1;
ch = getchar();
}
while(ch <= '9' && ch >= '0')
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(int x)
{
if(x > 9) print(x \/ 10);
putchar(x % 10 + '0');
}
struct note{
int s[3],tag; \/\/ s[0]:最小值之和, s[1]:计数, s[2]:贡献和
note() {s[0] = s[1] = s[2] = 0;}
}tr[maxn * 13];
#define lson (rt << 1)
#define rson (rt << 1 | 1)
#define mid ((l + r) >> 1)
void pushup(int rt)
{
for(int i = 0;i < 3;i++)
tr[rt].s[i] = tr[lson].s[i] + tr[rson].s[i];
}
void build(int rt,int l,int r)
{
if(l == r)
{
for(int i = 0;i < 3;i++) tr[rt].s[i] = 0;
tr[rt].tag = 0;
return;
}
build(lson,l,mid);
build(rson,mid + 1,r);
pushup(rt);
}
void pushdown(int rt)
{
if(tr[rt].tag)
{
\/\/ s[2] += tag * s[0] (最小值之和)
tr[lson].s[2] = tr[lson].s[2] + tr[rt].tag * tr[lson].s[0];
tr[rson].s[2] = tr[rson].s[2] + tr[rt].tag * tr[rson].s[0];
tr[lson].tag += tr[rt].tag;
tr[rson].tag += tr[rt].tag;
tr[rt].tag = 0;
}
}
void update(int rt,int l,int r,int x,int k,int id)
{
if(l == r)
{
tr[rt].s[id] = tr[rt].s[id] + k;
return;
}
pushdown(rt);
if(x <= mid) update(lson,l,mid,x,k,id);
else update(rson,mid + 1,r,x,k,id);
pushup(rt);
}
void upd(int rt,int l,int r,int x,int y,int k)
{
if(x <= l && r <= y)
{
tr[rt].s[2] = tr[rt].s[2] + k * tr[rt].s[0];
tr[rt].tag += k;
return;
}
pushdown(rt);
if(x <= mid) upd(lson,l,mid,x,y,k);
if(y > mid) upd(rson,mid + 1,r,x,y,k);
pushup(rt);
}
note query(int rt,int l,int r,int x,int y)
{
if(x <= l && r <= y) return tr[rt];
pushdown(rt);
note res, lss, rss;
if(x <= mid)
{
lss = query(lson,l,mid,x,y);
for(int i = 0;i < 3;i++) res.s[i] += lss.s[i];
}
if(y > mid)
{
rss = query(rson,mid + 1,r,x,y);
for(int i = 0;i < 3;i++) res.s[i] += rss.s[i];
}
return res;
}
int siz[maxn],f[maxn];
void getroot(int u,int fat)
{
siz[u] = 1;f[u] = 0;
for(int v : G[u])
{
if(v == fat || vis[v]) continue;
getroot(v,u);
siz[u] += siz[v];
f[u] = max(f[u],siz[v]);
}
f[u] = max(f[u],tot - siz[u]);
if(f[u] < f[rt]) rt = u;
}
vector<int> vec;
int m,a[maxn * 3];
vector<int> q[maxn * 3];
int mi[maxn],mx[maxn];
void dfs(int u,int fa)
{
mi[u] = min(mi[fa],u);
mx[u] = max(mx[fa],u);
a[++m] = mx[u];
a[++m] = mi[u];
a[++m] = u;
vec.push_back(u);
for(int v : G[u]) if(!vis[v] && v != fa) dfs(v,u);
}
int getans(int root,int fa)
{
int res = 0;m = 0;
vec.clear();dfs(root,fa); \/\/ 求出子树信息
sort(a + 1,a + m + 1);
m = unique(a + 1,a + m + 1) - a - 1;
build(1,1,m);\/\/ 线段树建树是 O(size)
for(int i = 1;i <= m;i++) q[i].clear();
for(auto u : vec)
{
int wz = lower_bound(a + 1,a + m + 1,mx[u]) - a;
q[wz].push_back(u);\/\/ 离线扫描线
}
for(int i = 1;i <= m;i++)
{
for(int u : q[i]) \/\/ add
{
\/\/ u 作为 x
int mip = lower_bound(a + 1,a + m + 1,mi[u]) - a;
update(1,1,m,mip,1,1);
upd(1,1,m,1,mip,1);
\/\/ u 作为 l
if(mi[u] == u)
{
int p = lower_bound(a + 1,a + m + 1,u) - a;
update(1,1,m,p,u,0);
int ss = query(1,1,m,p,m).s[1];
update(1,1,m,p,ss * u,2);
}
}
for(int u : q[i]) \/\/ query
{
if(mx[u] == u)
{
int mip = lower_bound(a + 1,a + m + 1,mi[u]) - a;
res += query(1,1,m,1,mip).s[2] * u;
}
}
}
return res;
}
void divide(int u)
{
mi[u] = mx[u] = u;
ans += getans(u,u);
vis[u] = 1;
for(int v : G[u])
{
if(vis[v]) continue;
ans -= getans(v,u);
}
for(int v : G[u])
{
if(vis[v]) continue;
tot = siz[v];
f[rt = 0] = 1e9;
getroot(v,0);
divide(rt);
}
}
int solve()
{
n = read();
for(int i = 1;i < n;i++)
{
int u = read(),v = read();
G[u].push_back(v);
G[v].push_back(u);
}
tot = n;
f[rt = 0] = 1e9;
getroot(1,0);
getroot(rt,0); \/\/ 重新计算size
divide(rt);
print(ans);puts("");
return 0;
}
signed main()
{
\/\/ ios::sync_with_stdio(false);
\/\/ cin.tie(0);cout.tie(0);
int t = read();
while(t--)
{
solve();
\/\/ 清空
for(int i = 1;i <= n;i++) G[i].clear(),vis[i] = 0;
ans = 0;
}
return 0;
}
希望对你有所帮助。
本人 $900$ AC 祭,伟大的点分治!伟大的 ez_lcw!
祝各位 CSP - S rp++。

 鲁ICP备2025150228号
鲁ICP备2025150228号