题目描述
有一个 $n \times n$ 的网格,每个格子里有一个数字,第 $i$ 行第 $j$ 列的数字记为 $a_{i,j}$。
你需要从左上角的网格顶点走到右下角的网格顶点,每一步只能沿网格线向下或向右走,总共走 $2n$ 步,一个例子如图所示:
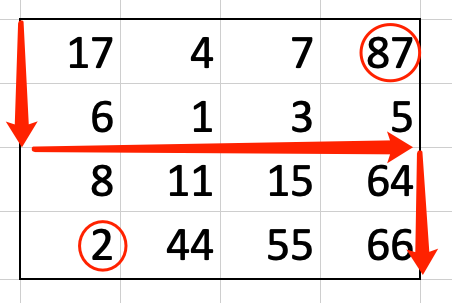
你的路径会将网格分成上下两部分,令 $A$ 表示路径右上方所有数字构成的集合,$B$ 表示路径左下方所有数字构成的集合,定义代价为 $\max\limits_{x \in A} \max\limits_{y \in B} |x-y|$。
特别的,若 $A,B$ 其中之一为空集,则定义代价为 $+\infty$。
你需要找到一条路径,最小化代价。
输入格式
第一行一个整数 $n$。
接下来 $n$ 行,每行 $n$ 个整数,第 $i$ 行第 $j$ 列的数表示 $a_{i,j}$。
输出格式
输出一行一个整数表示答案。
样例
样例 #1 输入
4
17 4 7 87
6 1 3 5
8 11 15 64
2 44 55 66样例 #1 输出
85样例 #1 解释
如图所示。
数据范围与约定
对于所有数据,有:
- $2 \le n \le 500$
- $1 \le a_{i,j} \le 10^9$
| 子任务 | 特殊性质 | 分值 |
|---|---|---|
| $1$ | $a_{i,j} \le 1$ | $20$ |
| $2$ | $a_{i,j} \le 2$ | $20$ |
| $3$ | $n \le 2$ | $20$ |
| $4$ | $n \le 10$ | $20$ |
| $5$ | 无 | $20$ |

 鲁ICP备2025150228号
鲁ICP备2025150228号