题目描述
给出一棵有 $2^K-1$ 个节点的完全二叉树,遍历这棵树的规律如下:
起点是二叉树第一层的唯一一个节点。
如果当前节点的左孩子还没有记录到,那么就记录左孩子的编号并移动到左孩子处。
如果当前节点没有左孩子或者左孩子已经记录过,就记录当前节点的编号。
如果当前节点已经记录过,那么就记录右孩子的编号并移动到右孩子处。
如果当前节点及此节点的左右孩子都已经记录过,那么就移动到当前节点的父节点处。
现在给出从第一层的节点出发记录下的编号顺序,请你求出原本的完全二叉树。
输入格式
第一行,一个整数 $K$,表示这个完全二叉树有 $2^K-1$ 个节点;
第二行,$2^K-1$ 个整数,表示从第一层的节点出发记录下的编号顺序。
输出格式
输出共 $K$ 行,为原本的完全二叉树。
输入输出样例 #1
输入 #1
2
2 1 3输出 #1
1
2 3输入输出样例 #2
输入 #2
3
1 6 4 3 5 2 7输出 #2
3
6 2
1 4 5 7说明/提示
【样例解释 #1】
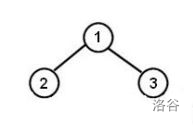
先移动到节点 $1$,发现左孩子没有记录,移动到节点 $2$ 并记录节点 $2$;发现节点 $2$ 没有孩子,返回节点 $1$ ,发现此节点没有记录,记录节点 $1$;发现右孩子没有记录,移动到节点 $3$ 并记录节点 $3$。
【样例解释 #2】
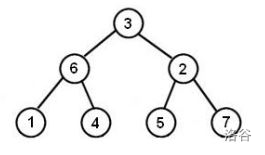
【数据范围】
对于 $100\%$ 的数据,$1\le K\le 10$。
【说明】
本题分值按 COCI 原题设置,满分 $80$。
题目译自COCI2013_2014 CONTEST #5 _T2 OBILAZAK_

 鲁ICP备2025150228号
鲁ICP备2025150228号