题目描述
为了让直升机能够降落在建筑物屋顶上,需要构建直升机着陆场。直升机着陆场必须满足以下所有条件:
- 直升机着陆场由 $k$ 个($k \geq 1$)同心圆组成。
- 构成直升机着陆场的每个圆的半径为 $1, 2, \dots, k$(是 $1$ 到 $k$ 之间的互不相同的自然数)。
- 每个圆的圆周必须用某一种颜色的油漆涂上。
直升机着陆场的“大小”指的是同心圆中最大圆的半径,根据上面的定义可以得出这等同于圆的个数 $k$。
如果两个直升机着陆场不同,意味着它们的大小不同,或者虽然大小相同,但圆周所用的颜色组合不同。
为了涂上半径为 $r$ 的圆的圆周,需要恰好 $r$ 桶该颜色的油漆。
例如,假设你有 3 桶红色油漆和 4 桶蓝色油漆,在这种情况下可以制作的不同的直升机着陆场如下图所示,共有 9 种不同的组合。图中的 X 表示同心圆的中心。
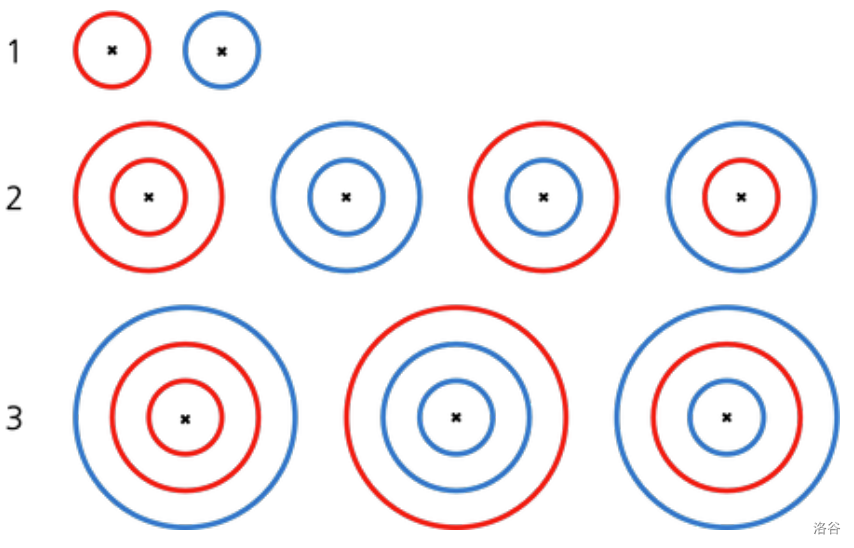
其中,若想绘制图中所示大小为 3 的某种着陆场,需要红色油漆 $4 = 1 + 3$ 桶和蓝色油漆 2 桶。但由于红色油漆只有 3 桶,因此这种着陆场无法制作。
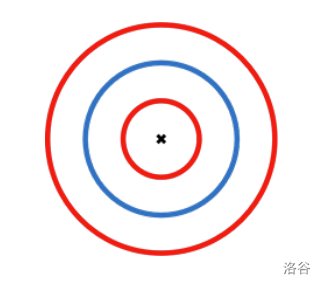
你现在拥有 $a$ 桶红色油漆和 $b$ 桶蓝色油漆。请你编写一个程序,计算仅使用这些油漆能够制作的不同的直升机着陆场的种类数,结果对 $10^9 + 7$ 取模。
一个输入包含 $T$ 个测试用例。你需要依次解决这 $T$ 个测试用例。
输入格式
第一行输入一个整数 $T$,表示测试用例的数量。
接下来 $T$ 行,每行包含两个整数 $a$ 和 $b$,中间用一个空格隔开,分别表示红色油漆和蓝色油漆的桶数。
输出格式
对于每个测试用例,输出一行,仅包含一个整数,表示使用给定数量的红色和蓝色油漆能够构造的不同的直升机着陆场数量,对 $10^9 + 7$ 取模。
输入输出样例 #1
输入 #1
3
3 4
10 5
7 12输出 #1
9
25
40说明/提示
约束条件
- 所有给定的数值均为整数。
- $1 \leq T \leq 10\,000$
- $1 \leq a, b \leq 50\,000$
子任务
- (3 分)$T = 1$, 且 $a, b \leq 6$
- (17 分)$T = 1$, 且 $a, b \leq 100$
- (21 分)$T = 1$, 且 $a, b \leq 1\,000$
- (23 分)$T = 1$, 且 $a, b \leq 5\,000$
- (26 分)$T = 1$
- (10 分)无额外约束条件

 鲁ICP备2025150228号
鲁ICP备2025150228号